Mathématiques 2: Statistiques :
Éstimation ponctuelle et par intervalle

1. Définitions

Le but de l'estimation en statistques est, à partir des paramètres comme la moyenne, la variance, ou la proportion calculés sur un échantillon, d'estimer ceux d'une population entière.

L'estimation est la réciproque de l'échantillonnage. On utilise les résultats établis sur la théorie de l'échantillonnage, c'est à dire, de la distribution d’échantillonnage, pour estimer ceux de la population parente.

Il s'agit bien d'utiliser des observations faites sur un échantillon et de tirer des conclusions sur la population toute entière. C'est approche qui n'est pas déductive, qui va du général au particulier, mais plutôt d'une démarhe statistique inductive ou inferentielle.

En théorie de l’estimation, on distingue les concepts suivants:

• les paramètres de la population comme la moyenne μ ou la variance σ² dont les valeurs sont certaines mais inconnues.

• les résultats de l’échantillonnage comme la moyenne m ou la variance s² dont les valeurs sont certaines et connues.

• les variables aléatoires des paramètres, comme la moyenne aléatoire 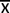dont la valeur est incertaine et dont la loi de probabilité est souvent connue.

Nous étudierons deux cas : celui où estime la moyenne μ d'une variable aléatoire définie sur une population et celui où l'on estime la proportion d'individus p ayant un certain caractère dans la population.

Pour estimer les paramètres de la loi de probabilité, la méthode utilisée est dite méthode du maximum de vraisemblance lorsque la distribution de la variable aléatoire X est connue. Si la distribution n'est pas connue, on utilise la méthode des moindres carrés.

2. Estimation ponctuelle

2.1. Définition

L’estimation d’un paramètre quelconque est ponctuelle si elle ne prend qu'une seule valeur.

L'estimation d'un paramètre, c'est sa valeur estimée. Elle est appelée estimateur du paramètre.

On estime un paramètre inconnu d'une population à partir des données observables sur un échantillon aléatoire.

On note θ̂ l'estimateur du paramètre θ .

L’estimation par intervalle associe à un échantillon aléatoire, un intervalle [θ̂₁,θ̂₂] qui recouvre θ avec une certaine probabilité.

2.2. Estimateur des deux paramètres μ
et σ² d'une loi normal N(μ,σ²)

On considère une loi normale N(μ, σ) sur une population dont la valeur des paramètres μ n’est pas connue pour laquelle on souhaite estimer l’espérance μ.

Soient X une variable aléatoire continue suivant cette loi normale et X1 , X2 ,…, Xi , ..., Xn , n réalisations indépendantes de la variable aléatoire X.

Un estimateur du paramètre θ est une variable aléatoire θ̂ fonction des Xi.

L'estimateur θ̂ du paramètre θ obéit aux deux relations suivantes:

E (θ̂) = θ et
V(θ̂) est minimale.

On notera :

μ̂ l'estimateur de μ et
σ2̂ l'estimateur de σ².

On cherche μ̂ et σ2̂ de telle sorte que:

E (μ̂ ) = μ et V(μ̂ ) soit minimale ; puis

E (σ2̂) = σ² et V(σ2̂) soit minimale.

Un estimateur du paramètre μ est une variable aléatoire μ̂ fonction des Xi.

On utilse la méthode des moindres carrés qui consiste à rechercher les coefficients de la combinaison linéaire μ̂ = c1 X1 + c2 X2 +... + ci Xi + ... + cn Xn

telle que

E (μ̂ ) = μ et V(μ̂ ) soit minimale.

Nous avons X̄ = ΣXi/n. Donc E(X̄) = μ

μ, est l'espérance de la loi de probabilité de la variable aléatoire X.

Ainsi

μ̂ = X̄ = ΣXi/n,

La moyenne arithmétique constitue le meilleur estimateur de μ.

μ̂ = X̄ = ΣXi/n.

Soit X une variable aléatoire continue suivant une loi normale N (μ,Σ) pour laquelle on souhaite estimer la variance Σ².

Soient X1 , X2 ,…, Xi , ..., Xn , n réalisations indépendantes de la variable aléatoire X.

Un estimateur σ2̂ du paramètre σ² est une fonction des variables aléatoires Xi : σ2̂ = f (X1 , X2 ,…, Xi , ..., Xn)

Nous avons deux cas:

1. Cas où l’espérance μ est connue

On utilse la méthode des moindres carrés qui consiste à rechercher les coefficients de la combinaison linéaire σ2̂ = c1(X1 - μ)2 + c2(X2 - μ)2 + ... + ci(Xi - μ)2 + ... + cn ( Xn - μ)2

telle que

E (σ2̂) = σ² et
V(σ2̂) soit minimale.

La variance de la loi de probabilité de la variable aléatoire X est la variance observée. C'est le meilleur estimateur de σ² lorsque μ est connue:

σ2̂ = (1/n)Σ(Xi - μ)².


2. Cas où l’espérance μ est inconnue

On estime μ à μ̂ = X̄ et on calcule la variance observée S²:

S² = (1/n) Σ (Xi - X̄)² = (1/n) Σ (Xi - μ + μ - X̄)²
= (1/n) Σ (Xi - μ - (X̄) - μ)² = (1/n) Σ (Xi - μ)² - 2 X̄ -μ)(1/n) Σ(Xi - μ) + (X̄ - μ)² =
(1/n) Σ (Xi - μ)² - 2 (X̄ - μ) ² + (X̄ - μ)² = (1/n) Σ (Xi - μ)² - (X̄ - μ)²

(1/n) Σ (Xi - μ)² est la variance de la population = σ². Ainsi

(X̄ - μ)² = (Σ Xi/n - (1/n) n μ)² =
(1/n²)(Σ Xi - Σμ)² = (1/n) (1/n)(Σ Xi - Σμ)² = (1/n) σ²

Ainsi

S² = σ² - (1/n) σ² = [(n - 1)/n]σ²

Finalement,

S² = σ² - (1/n) σ² = σ² = [n/(n - 1)] S²

Le meilleur estimateur de σ² σ2̂, variance de la loi de probabilité de la variable aléatoire X associée à la population lorsque l’espérance μ est inconnue est :

σ2̂ = [n/(n - 1)]S² =
[1/(n - 1)]Σ(Xi - X̄)²

On remarque que lorsque n tend vers l'infini n/(n - 1) tend vers 1, et donc σ2̂ = S². La variance observée S² tend vers la variance de la population σ².

La valeur de ε_α est donnée par la table de l’écart-réduit pour une valeur α donnée.

Coefficient de risque α	Ecart-réduit εα
0,01	2,576
0,05	1,960
0,10	1,645

2. cas ou X tend vers la loi N(μ,σ), n est quelconque, σ₂ est inconnue

Comme pour l'estimation ponctuelle on estime la variance de la population à

σ̂² = [n/(n - 1)]S².

S² est la variance de l'échantillon.

On estime donc la moyenne X̄ comme suit:

P(- c/(σ̂ /√n) < (X̄ - μ)/(σ̂ /√n) < + c/(σ̂/√n)) =
1 - α

Avec (X̄ - μ)/(σ̂/√n) → T(ddl = n - 1)

T(ddl = n - 1) est la loi de Student pour un ddl = n - 1.

Ainsi |c/(σ̂/√n))| correspond à la valeur t_α de la variable de Student pour un ddl = n - 1, et pour la probabilité α donnée.

Nous avons donc

t_α = |c/(σ̂/√n)|, ou c = t_α σ̂/√n

Lorsque n < 30, la loi de student converge vers une loi normale réduite. Ainsi La valeur de t_α(n-1) est égale à celle de l'écart réduit ε_α

Exemple pour un risque α = 0,05

Taille de l’échantillon n	Ecart-réduit εα	Variable DE student tα
10	1.960	2.228
20	1.960	2.086
30	1.960	2.042
40	1.960	1.960

3. cas ou X suit une loi inconnu et n > 30

Puisque par définition la variance de la population est inconnue, elle doit donc être estimée avec la variance observée comme pour le cas précédent:

σ2̂ = [n/(n - 1)]S²

la loi suivie par la variable centrée réduite

(X̄ - μ)/(σ̂/√n) → N(0,1)

4. cas ou X suit une loi inconnuE et n < 30



La loi de probabilité suivie par (X̄ - μ)/(σ̂/√n) n’est pas connue. Dans ce cas, on a recours aux statistiques non paramétriques.

2.3. Intervalle de confiance d’une proportion

L’intervalle de confiance autour de la fréquence p de la population à partir de son estimateur K/n correspond à la valeur de c pour une valeur du coefficient de confiance (1 - α) telle que :

P(K/n - c < p < K/n + c ) = 1 - α

ou

P(p - c < K/n < p + c ) = 1 - α

On a aussi

P( - c < K/n - p < c ) = 1 - α

P( - c/√(p(1 - p)/n) < (K/n - p)/√(p(1 - p)/n) < c/√(p(1 - p)/n)) = 1 - α

Avec (K/n - p)/√(p(1 - p)/n) → N(0,1)

La valeur |c/√(p(1 - p)/n)| est la valeur de la variable normale réduite pour la probabilité α donnée appelée aussi écart réduit et notée ε_α.

On estime la variance V(K/p) = pq qui est inconnue par p̂q̂/n

avec

q = 1 - p

p̂ = K/n, et q̂ = (n - K)/n