Statistiques
Statistiques
descriptives
Échantillonage
Éstimation
Statistiques
inférentielles
Statistiques
Calculateurs
© The scientific sentence. 2010
|
Mathématiques 2: Statistiques:
Intervalle de fluctuation
Intervalle de confiance
1. Défnition d'un intervalle de fluctuation

À partir d'un verger d'orangers, on acceuille un échantion de
80 oranges dans le but de connaître leur masse et d'améliorer
leur qualité. On trouve les valeurs ci-contre.:
Question:
Maintenant, si on répète le même expérience, trouve-t-on
les mêmes valeurs que celles déjà obtenues?
Réponse: Non, mais légèrement différentes.
Ces différences dans les valeurs mesurées sont dites
fluctuactions des valeurs considérées.
Ces fluctuations sont dues à l'échantillonnage lui même,
au moyens d'effectuer l'expérience, ...
Toutes ces valeurs fluctuantes se trouvent à l'intérieur
d'un intervalle de fluctuation.
En statistiques, un intervalle de fluctuation sert à établir la marge d'erreur entre les données d'un échantillon (sondage) et les données de la population totale.
Lorsque la population est vaste, avec des milliers d'individus, il est plus rapide de travailler sur un échantillon et d'étendre les résultats à l'ensemble.
Le fait de travailler sur un petit échantillon issu d'une grande population mène
sûrement à des erreurs. L'intervalle de fluctuation précise alors une marge
d'erreur pour toutes les grandeurs observées .
Les grandeurs observées sont les grandeurs expérimentales mesurées.
À partir de ces mesures, on établit d'autres valeurs centrales,
ou de position.
On détermine un intervalle de fluctuation principalement pour une moyenne ou pour une proportion .
La fréquence , ainsi que la probabilité sont des
proportions.
L'objectif est donc de préciser, à partir des mesures effectuées sur
l'échantillon, selon l'intervalle de fluctuation, la valeur ou
la proportion du caractère d'un individu dans la population.
2. Calcul d'intervalle de fluctuation
Nous allons établir l'expression de intervalle de fluctuation
pour la valeur de la mesure d'une grandeur g . La grandeur g est une moyenne 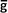 ou une proportion. ou une proportion.
• Pour établir un intervalle de fluctuation, on doit tout d'abord connaître,
ou admettre la valeur de la grandeur g du caractète étudié dans la population .
• On sélectionne un échantillon de taille n parmi tous
les individus de la population. C'est à partir de cet échantillon que
se feront tous nos calculs.
• On Calcule la moyenne 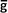 de la grandeur g, et l'écart-type σ de cet échantillon. de la grandeur g, et l'écart-type σ de cet échantillon.
• On choisi un seuil pour la grandeur g.
Un seuil de la grandeur g est
le pourcentage s% qui détermine la marge d'erreur. Ainsi
le risque α est de (100 - s)%.
α =
1 - s%.
Au seuil de s% en grandeur g
avec une marge d'erreur inférieure à α.
Les seuils les plus couramment utilisés sont 10%, 5% et 1%. Souvent, on travaille avec 5%.
• À partir de ce seuil de risque α, on trouve le coefficient de confiance Z(α) au moyen des tables ou logiciel.
Voici les coefficients de risque et leurs ecart-réduits que
l'on utilise souvent:
Z(0.01) = 2.576
Z(0.05) = 1.960
Z(0.10) = 1.645
• La marge d'erreur ME se calcule alors par la formule suivante
ME =
Z(α) x
• L'intervalle de fluctuation est:
I = [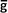 (admise) -
Z(α) x ; (admise) -
Z(α) x ;
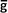 (admise) +
Z(α) x ] (admise) +
Z(α) x ]
3. Défnition d'un intervalle de confiance
En statistiques, tout comme un intervalle de fluctuation, un intervalle de confiance sert à établir la marge d'erreur entre les données d'un échantillon et les données de la population totale.
L'intervalle de fluctuation est relatif à l'échatillon, mais l'intervalle de confiance est relatif plutôt à la population.
Lors d'une expérience réalisée sur UN échantillon, on obtient une valeur
pour la grandeur g. À partir de ce résultat on établit un intervalle de confiance afin de situer la grandeur g
de la population.
On détermine un intervalle de confiance principalement pour une moyenne ou pour une proportion .
La fréquence , ainsi que la probabilité sont des
proportions.
L'objectif est donc de préciser, à partir des mesures effectuées sur
l'échantillon, selon l'intervalle de confiance, la valeur
ou la proportion du caractère d'un individu dans la population.
4. Calcul d'intervalle de confiance
Nous allons établir l'expression de intervalle de confiance
pour la valeur de la mesure d'une grandeur g . La grandeur g est une moyenne 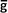 ou une proportion. ou une proportion.
• Pour établir un intervalle de confiance, on doit tout d'abord, à
partir d'une expérience sur UN échantillon, mesurer la
déterminer la valeur de la grandeur g du caractète étudié dans la population .
g. Cette valeur sert à corriger la valeur g admise
dans la poulation slon l'intervalle de confiance.
• On pocède de la même façon que pour le calcul
de la marge d'erreur pour l'intervalle de fluctuation.
Ici, le seuil s% de la grandeur g qui détermine la marge d'erreur est appellé degré de confiance. Ainsi
le risque α est de (100 - s)%.
α =
1- s% .
• La marge d'erreur ME se calcule alors par la formule suivante
ME =
Z(α) x
• L'intervalle de confiance est:
I = [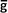 (observée) -
Z(α) x ; (observée) -
Z(α) x ;
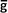 (observée) +
Z(α) x ] (observée) +
Z(α) x ]
|
|