Statistiques
Statistiques
descriptives
Échantillonage
Éstimation
Statistiques
inférentielles
Statistiques
Calculateurs
© The scientific sentence. 2010
|
Mathématiques 2: Statistiques:
Intervalle de fluctuation
Intervalle de confiance
1. Intervalle de fluctuation : Exemple

Dans l'exemple des oranges, la grandeur considérée est la masse des oranges:
• La grandeur à estimer dans la population des oranges est connue: 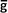 admise = 200 g. admise = 200 g.
• La taille de l'échantillon est n = 80.
• On prend un seuil de risque de 0.05, donc Z(0.05) = 1.960.
• L'écart-type σ = 1.67
La marge d'erreur ME est donc:
ME = 1.960 x 1.67/√80 = 0.366
L'intervalle de fluctuation est:
I = [200 - 0.37 ; 200 + 0.37]
2. Intervalle de confiance Exemple
On adopte la procédure d’estimation suivante :
Pour estimer la masse d'un abricot au sein de sa population, on prélève UN
échantillon aléatoire de taille n = 80 pour lequel on obtient UNE masse moyenne. La masse moyenne inconnue d'un abricot dans la population mère est dans l’intervalle
de confiance que nous allons calculer.

Pour l'exemple d'un verger d'abricotiers, la grandeur considérée est la masse des oranges. On a les résultats ci-contre:
• La grandeur à estmer dans la population des abricots est inconnue 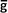 admise = 200 g. admise = 200 g.
• 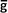 mesurée = 60.1 g. mesurée = 60.1 g.
• La taille de l'échantillon est n = 80.
• On prend un seuil de risque de 0.05, donc Z(0.05) = 1.960.
• L'écart-type σ = 1.74
La marge d'erreur ME est donc:
ME = 1.960 x 1.74/√80 = 0.38.
L'intervalle de confiance est:
I = [60.1 - 0.38 ; 60.1 + 0.38]
C'est l'intervalle de confiance de la masse d'un abricot au niveau de
confiance 95%.
3. Intervalle de fluctuation
pour une épreuve de Bernoulli
Si Xn une variable aléatoire qui suit la loi binomiale B(n;p) avec les conditions suivantes:
• 0 < p < 1,
• n ≥ 30,
• np et n(1 - p) ≥ 5.
avec
• La taille de l'échantillon est n .
• un seuil de risque α
• L'écart-type σ = √p(1 - p)
La marge d'erreur ME est donc:
ME = Z(α) x √p(1 - p)/√n.
l'intervalle de fluctuation asymptotique (ou approché)
de la variable fréquence du nombre de succès: Xn au seuil de α est :
I = [p - Z(α) x √p(1 - p)/√n ;
p + Z(α) x √p(1 - p)/√n.]
4. Intervalle simplifié de fluctuation
pour une épreuve de Bernoulli
• Si 0 ≤ p ≤ 1 alors p(1 - p) est toujours ≤ 1/4.
Il suffit de tracer le graphe de le fonction f(p) = p (1 - p)
pour s'en apecevoir. Donc:
√ p(1 - p)/√n < 1/2√n.
• Si, en plus, α = 0.05 alor Z(α) = 1.96 ≈ 2.
On a donc une approximation de ME:
ME = 1.96 x 1/2 √n = 1/√n
![]()
On résume donc:
Pour une variable aléatoire Xn qui suit la loi binomiale B(n;p) avec les conditions suivantes:
• 0 < p < 1,
• n ≥ 30,
• np et n(1 - p) ≥ 5.
Avec:
• Le seuil de risque α est de 0.05 ou (1 - α = 95%)
• La taille de l'échantillon est n .
La marge d'erreur ME est donc:
ME = 1/√n.
l'intervalle de fluctuation asymptotique (ou approché)
de la variable fréquence du nombre de succès: Xn au seuil de α est :
I = [p - 1/√n ; p + 1/√n]
5. Intervalle simplifié de fluctuation
pour un pile ou face
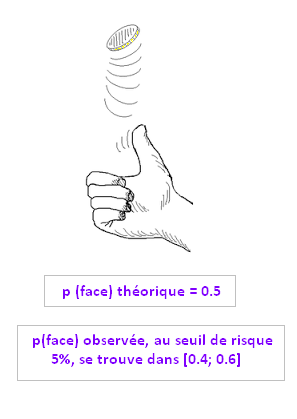
Pour un lancer, répépté n = 81 fois d'une pièce de monnaie équilibrée, la
proportion, ou probabilité d'une face étant p = 1/2 = 0.5;
l'intervalle de fluctuation approché de la fréquence du nombre de face au seuil de α = 0.05 est :
I = [1/2 - 1/9 ; 1/2 + 1/9] = [7/18; 11/18]
I = [0.4; 0.6]
|
|