Mathématiques: Statistiques : Test de Χ2

Le test de Χ2 (ki au carré) est utilisé pour se renseigner sur l'indépendence des caractères de deux échantions.

Il met en evidence le tableau de contingence contenant des données brutes qui sont des fréquences absolues, c'est à dire qui ne sont pas des fréquences relatives (en %).

Le test de Χ2 n'est pas utilsable lorsqu'il y a peu d'observations, ou sur un tableau de contingence lorsque une valeur attendue (ou espérance) est plus petite que 1; ou que 20% (ou plus) des espérances sont inférieures à 5. Lorsque c'est le cas, il faut regrouper les caractères.

1. Tableau de contingence

On veut savoir si la présence des pépins dans le raisin dépend de la couleur. Parmi 3 grapes, on goûte 100 raisins de couleur blanche, noire et rouge . Les resultas relatifs sont regroupés dans le tableau de contingence suivant:

raisin sans pépins avec pépins total

blanc 30 15 45

noir 15 20 35

rouge 15 5 20

total 60 40 100 = N

Ce tableau de contingence contenant les données brutes associe le caractère qualitatif contenir des pépins et le caractère qualitatif couleur.

Les valeurs de chaque case sont les valeurs observées ou mesurées. Ces valeures sont contingentes puisqu'elles peuvent évenuellement ou possiblement arriver ou ne pas arriver. En Statistiques, la contingence c'est la dépendance ou la liaison entre deux caractères généralement qualitatifs.

Le total des lignes et le total des colonnes sont appelés totaux marginaux.

N est le nombre total d'observations (100 raisins testés = 100).

A partir de ces données issues de l’observation on construit un autre tableau de contingence qui contiendra les valeurs calculées, dites théoriques ou attendues ou espérées , sous l’hypothèse d’indépendance des deux caractères (ici contenace de pépins et couleur).

2. L'indépendance de caractères

L'indépendance des caractères est le fait que l'un des caractères est le même pour tout son groupe pendant que l'autre caractère ne l'est pas.

Si la contenance en pépins n'était pas influencée par la couleur, on aurait dans chaque case (ou pour chaque effectif) son total marginal multiplié par la probabilité pour qu'il soit ainsi.

Par exemple pour 30 raisins blancs sans pépins, on aurait plutôt 45 x 60/100 = 27. Cette valeur est appelée espérance.

3. Calcul des espérances

L'espérance ou la valeur espérée est la valeur attendue au cas où les caractères sont indépendants.

A partir du tableau de contingence des données observées, on construit donc un nouveau tableau de contingence qui contient les espérances; sous l’hypothèse d’indépendance des deux caractères:

raisin sans pépins avec pépins total

blanc 45x60/100 = 27 45x40/100 = 18 45

noir 35x60/100 = 21 35x40/100 = 14 35

rouge 20x60/100 = 12 20x40/100 = 8 20

total 60 40 100 = N

Dans chaque case, on a calculé le nombre d'observations qu'on aurait eu si la contenance en pépins n'était pas influencée par la couleur.

Le nombre total et les totaux marginaux sont concervés.

Nous avons donc deux tableaux. Celui des données observées et celui des données théoriques avec l'hypothèse que les deux caractères présence de pépins et couleurs sont indépendants.

4. L'hypothèse d'indépendance

Maintenant, on considère que l'hypothèse d'indépendance des deux caractères est vraie. Cette hypothèse doit donc être testée. On fait un test sur les deux tableaux. Ce test fait intervenir un paramètre décisif appelé Χ². Le Χ² théorique et le Χ² observé.

Si le paramètre théorique du test est plus grand que le paramètre observé, alors on garde l'hpothèse, sinon on rejette cette hypothèse et on accèpte son contraire.

Le paramètre théorique limite un intervalle de probabilités [o, α] dans lequel l'hypothèse est vraie. Le nmbre α est appelé seuil de confiance. Il peut prendre toutes les valeurs de probabilité entre 0 et 1. De coutume, on le prend égal à 5%.

La table de Χ2 donnera la probabilité 1 - 5% = 0.95.

Le paramètre théorique de Χ2 depend donc du risque α et du degré de liberté dll du problème.

dll = (nombre de lignes –1) x (nombre de colonnes –1)

Le paramètre observé de Χ2 se calcule selonn la formule suivante suivante:

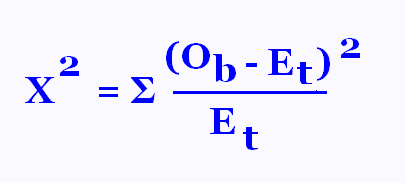
Ob est la valeur observée et Et la valeur théorique.

4. Χ² observé

À l'aide de la formule ci-dessus, on obtient:

raisin sans pépins avec pépins

blanc (30 - 27)²/27 = 0.33 (15 - 18)²/18 = 0.5

noir (15 - 21)²/21 = 1.71 (20 - 14)²/14 = 2.57

rouge (15 - 12)²/12 = 0.75 (5 - 8)²/8 = 1.12

1. Χ²(observé):

Χ²(observé) = 0.33 + 0.5 + 1.71 + 2.57 + 0.75 + 1.12 = 6.98

6. Χ² théorique et Décision

dll = (nombre de lignes –1) x (nombre de colonnes –1)
= (3 – 1) fois (2 –1) = 2

dll = 2

2. Χ²(théorique):

Avec α = 5% donc p (probabilité) = 1 - 0.05 = 0.95 et dll = 2, on a:

Χ²(théorique) = 6.02

Χ²(théorique) = 6.02 < Χ²(observé) = 6.98

L'hypothèse de l'indépendence est rejetée.

On peut donc affirmer avec un risque de se tromper inférieur à 0.5% que la présence de pépins et la couleur du raisin ne sont pas indépendantes.