Mathématiques 2: Statistiques
La loi normale

1. Exemple

On lance deux dés indiscernables à la fois. Le montant gagné correspond à la somme des nombres des deux faces obtenues.

Voici le diagramme des résultats possibles. À chaque somme (xi) correspond une probabilité (pi).

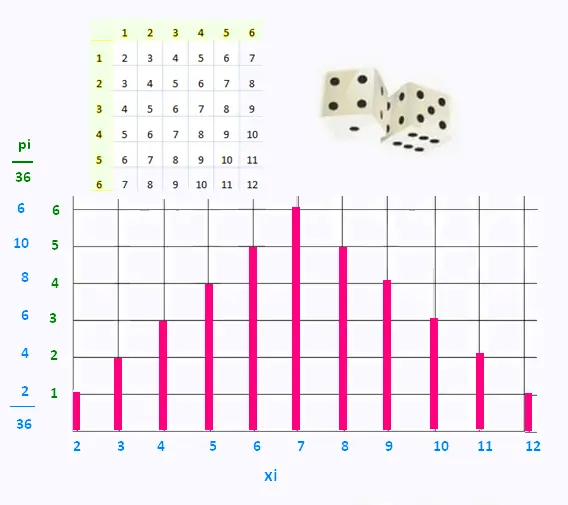
• Variable quantitative X = «somme des nombres des deux faces obtenues»
• 2 paramètres μ et σ.

On observe souvent en sciences des distributions similaires, symétriques autour de μ avec une forme de cloche

2. La loi normale centrée réduite

Pour faire des calculs, on suppose que la variable aléatoire X suit une distribution «patron» de la loi normale


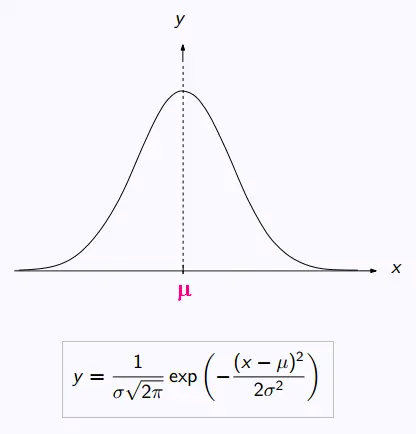
Pour chaque μ et σ, il existe une loi normale de moyenne μ et d'écart-type σ que l'on note N(μ;σ)

Si μ = 0 et σ = 1, la loi N(0,1) est dite loi normale centrée réduite .

Lorsque l’on suppose qu'une variable X suit le modèle de la loi normale N(μ,σ) on ecrit X ˜ N(μ;σ).

3. Exemple

On suppose qu'une certaine variable X ˜ N (0, 1). Pour quelle proportion d'individus a-t-on X ≤ 1.32 ? X > 1.32 ?

Réponse:

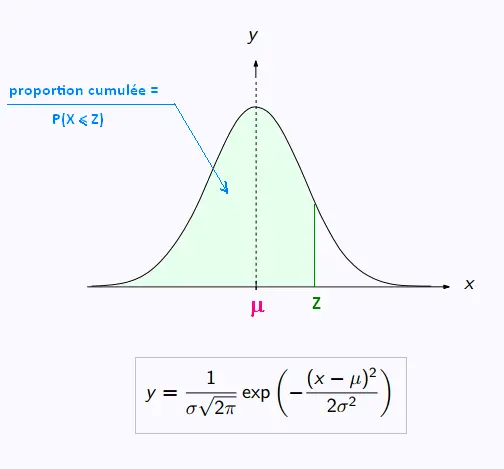
On cherche P(X ≤ 1.32). On utilse donc une table de la loi normale avec l'ecriture F(1.32).

On trouve F(1.32) = 0.906

Pour 90.60% des individus, la variable X est inférieure à 1.32.

P(X > 1.32) = 1 - P(X ≤ 1.32) = 1 - 0.906 = 0.04

Pour 4.00 % des individus, la variable X est supérieure à 1.32.

4. Loi normale quelconque

Pour faire des calculs avec une N(μ;σ), on se ramène à la loi N(0,1). C'est à dire on centre et on réduit X.

Théorème

Si X ˜ N(μ;σ) alors (X - μ)/σ ˜ N(0,1).

On suppose qu'une certaine variable X ~ N(7;3). Pour quelle proportion d'individus a-t-on X <12 ?

Réponse:

On cherche P(X ≤ 12).

On centre et on réduit X : (X - 7)/3 ~ N (0, 1).

P(X ≤ 12) = P((X - 7)/3 ≤ (12 - 7)/3) = P((X - 7)/3 ≤ 5/3) =
P((X - 7)/3 ≤ 1.76) = P(Z ≤ 1.76)

La table donne F(1,67) = 0.9608

P(X ≤ 12) = 96.08%