Statistiques
Statistiques
descriptives
Échantillonage
Éstimation
Statistiques
inférentielles
Statistiques
Calculateurs
© The scientific sentence. 2010
|
Mathématiques statistiques
Test graphique de Lilliefors
1. Le test de Lilliefors
La procédure du test de de Lilliefors est
la suivante:
1. Prélever un échantillon d'une population,
2. Ranger les valeurs xi par ordre croissant,
3. Déterminer les fréquences cumulées croissantes Fi,
4. Centrer et réduire les valeurs xi pour avoir les
Zi,
Moyenne: μ = Σxi ni /n
Variance: V = (Σnixi2/n) - μ2
Ecart-type: σ = √(V)
Normaliser l'évart-type: σo = (&adic;(n/(n - 1)))σ
Calculer les Zi = (xi - μ)/σo
5. Construire la fonction de répartition de l’échantillon sur le
papier de Lilliefors: Fréquences cumulées
Fi en fonction de Zi.
6. Prendre une décision suivant la courbe en escalier
de la fonction de répartition:
. Si les pas ne coupent pas les frontières : accepter la normalité,
. Si ils coupent les frontières : rejetter la normalité de la population.
Ces frontières sont définies par les courbes de Lilliefors
pour différentes valeurs n de la taille de l'échantillon.
2. Exemple
On fait un jus d'orange. Sur 20 oranges utilisées, on a
le tableau suivant:

| jus (mL) | 70 | 45 | 65 | 55 | 50 | 40 | 60 |
| effectifs | 2 | 3 | 5 | 3 | 2 | 1 | 4 |
Question:
La distribution observée des jus d'oranges d'une
population d'oranges est-elle
compatible avec la loi normale?
Réponse:
La variable aléatoire, c'est la quantité de jus à prélever.
La quantité, en mL, de jus obtenu pour chaque orange est
la valeur de cette variable aléatoire.
Cette variable aléatoire sera noté X, sa valeur x.
On trie le tableau dans l'ordre croissant selon les
mL de jus, on calcule les fréquences, puis les fréquences
cumulées. On a le nouveau tableau suivant:
| x | 40 | 45 | 50 | 55 | 60 | 65 | 70 |
| effectifs | 1 | 3 | 2 | 3 | 4 | 5 | 2 |
| fréquences | 1/20 | 3/20 | 2/20 | 3/20 | 4/20 | 5/20 | 2/20 |
fréquences
cumulées | 1/20 | 4/20 | 6/20 | 9/20 | 13/20 | 18/20 | 20/20 |
Une fréquence cumulée, par exemple 9/20,
représente le pourcentage d'oranges qui prennent une valeur
inférieure ou égale à 9.
Nous avons les paramètres suivants:
Effectif total = 20
μ = 57.25
V = 76.19
σ = 8.73
σo = (√(20/19)) x 8.73 = 8.96
Zi = (xi - μ)/σo
| x | 40 | 45 | 50 | 55 | 60 | 65 | 70 |
| Zi | - 1.92 | - 1.37 | - 0.81 | - 0.25 | + 0.32 | 0.86 | 1.42 |
fréquenses
cumulées | 1/20 | 4/20 | 6/20 | 9/20 | 13/20 | 18/20 | 20/20 |
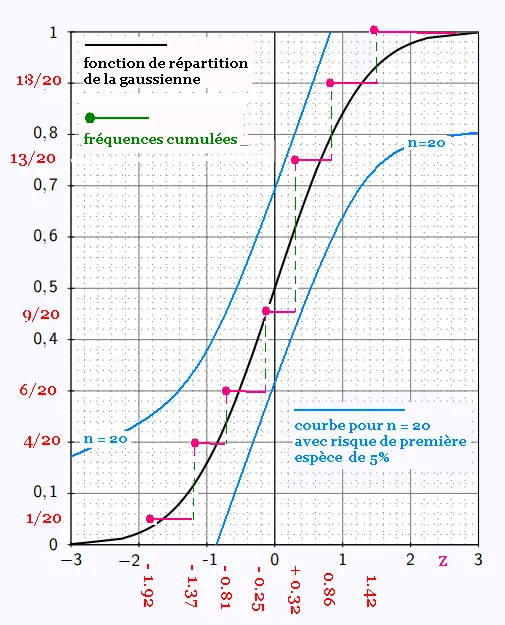
La fonction de répartition de l'échantillon de taille n = 20 reste entre les courbes n = 20.
On accèpte la
normalité de la poulation
.
|
|