Statistiques
Statistiques
descriptives
Échantillonage
Éstimation
Statistiques
inférentielles
Statistiques
Calculateurs
© The scientific sentence. 2010
|
Mathématiques 2: Statistiques :
Théorème central-limite
On rappelle qu'en théorie des probabilités, une variable aléatoire est une application définie sur l'ensemble des éventualités, c'est-à-dire l'ensemble des résultats possibles d'une expérience aléatoire.
1. Théorème central-limite (TCL)
Le TCL énonce que les moyennes des moyennes d'un grand nombre d'échantillons
suivent une loi normale, même si ces échantillons suivent individuellement une
autre loi de probabilité.
En statistique inférentielle, ce théorème qui permet le calcul des
intervalles de confiance autour des estimateurs.
2. Expression formelle du TCL
Soit une suite de variables aléatoires X1, X2, …, Xs indépendantes et de même
loi, c'est à dire de même espérance m et de même écart-type σ.
Soit 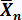 la moyenne des variables aléatoires Xi. la moyenne des variables aléatoires Xi.
On recalcule cette moyenne 1, 2, ou 3, ... , ou n fois. À chaque fois, on note
la moyenne Yn. On obtient une nouvelle série statistique,
constituée des moyennes observées à chaque fois.
Soit Y la variable aléatoire «moyenne» . Sa valeur, moyenne des
moyennes, converge en loi, lorsque n est grand, vers la loi normale centrée
réduite N(0,1):
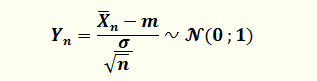
On peut dire donc:
La moyenne d'un gros échantillon aléatoire suit la loi normale.
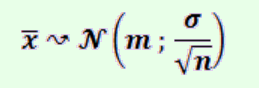
Remarque:
La moyenne des moyennes, la variable aléatoire,
Yn peut bien prendre les formes
suivantes:
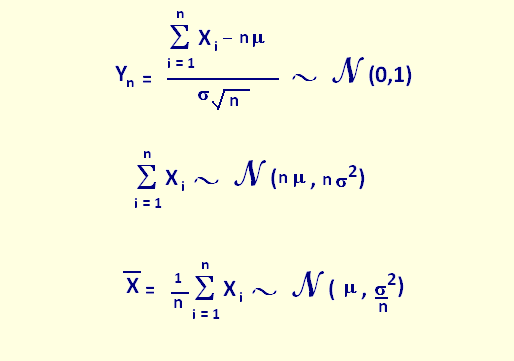
3. Cas général du TCL
En fait, c'est Y∞ qui est la loi normale, mais
on pratique, on admet qu'à compter d'un échantillon de 30 moyennes
la loi normale peut être utilisée. Lorsqu'il y a des valeurs aberrantes,
ou les distributions asymétriques, on retient
plutôt un minimum de 50.
Remarque: La variable aléatoire Yn peut bien s'ecrire sans
le radical √n et suivre donc la loi normale N(0,√n):
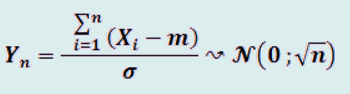
Soit une suite de variables aléatoires indépendantes X1, X2, …, Xn,
avec E(Xi) = νi et V(Xi) = σi2,
pour i = 1,2,3, ..., n.
Pour n grand, on a:
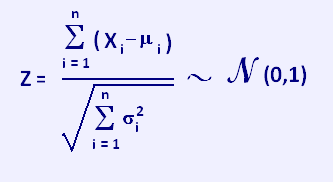
|
|