Mathématiques 2: Statistiques :
Distribution d’échantillonnage

1. Distribution d’échantillonnage

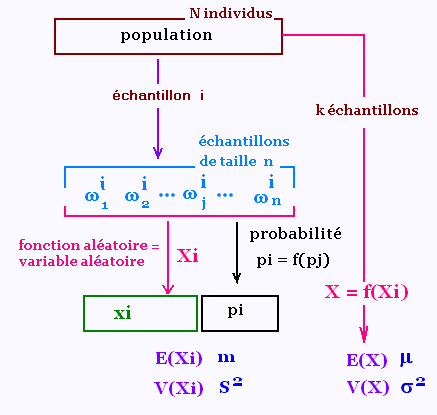
Soit une population de N individus. On extrait un echantillon aléatoire de taille n. On l'observe et puis on le remet ou non dans la population.

On repète k fois la même expérience en extrayant à chaque fois un échantillon aléatoire de même effectif n.

La population est caractérisée par ses paramètres μ(espérance) σ²(variance), p (probabilité), et X (variable aléatoire).

L'échatillon i est caractérisée par mi (espérance) s²i (variance), fi (probabilité), et Xi (variable aléatoire).

Le résultat d'un tirage aléatoire de l'échatillon i donnent n objets ou n caractères ωi. A ce caractère, de fréquence fi, on lui associe au moyen de la fonction ou de la variable aléatoire Xi, un réel xi. L'objet ωi est donc transformé en loi de probabilité P(xi, fi).

Cette loi de probabilité P(xi, pi) est nécessaire au calcul de l'espérance et de la variance pour la variable aléatoire X de la population.

Pour la variable aléatoire Xi de l'échantillon de taille n, on calcule ses paramètres descriptifs (fi, mi, s²i).

Pour chaque échatillon i, on obtient ainsi des paramètres estimés comme la moyenne mi.

Au total, nous avons k valeurs de chaque paramètre estimé comme mi: {m1, m2, m3, ..., mi, ..., mk}.

Cette série statistique composée de k éléments correspondant au k estimations du paramètre étudié. Elle est appelée distribution d'échantillonnage du paramètre, comme la distribution d'échantillonnage de la moyenne.

À cette série statistique {mk}, paramètres résultant de chaque échantillon, on associe une nouvelle variable aléatoire Y à chacun des paramètres mi de probabilité pi(comme la moyenne des moyennes). On obtient ainsi une nouvelle loi de probabilité P(mi,pi) associée à la variable aléatoire Y = f(X1, X2, ..., Xi, ...Xk) et relative à la population.

La loi de probabilité P(mi, pi) suivie par cette variable aléatoire Y admet comme distribution, la distribution d’échantillonnage du paramètre mi auquel on pourra associer une espérance et une variance.

Dans la pratiqoe, on prend un seul échantillon. L'échantillon prélevé de la population doit être le mieux représentatif possible. Les n observations x1 , x2 ,…, xi , ..., xn, faites sur l'échantillon snt considérées comme n variables aléatoires X1 , X2 ,…, Xi , ..., Xn.

A partir de ces n variables aléatoires, on défini une nouvelle variable Y qui sera fonction de ces dernières :

Y = ƒ(X1, X2, …, Xi , ..., Xn )

2. Loi de probabilité de la moyenne

Soit X la variable aléatoire suivant une loi normale d’espérance μ et de variance σ².

Soient n copies indépendantes X1, X2,…, Xi,…, Xn telle que Xi est la varaible indépendente associée au ième élément de chacun des n éléments de l'échantillon avec E(Xi) = μ et V(Xi) = σ².

On construit la variable aléatoire X̄, telle que:

X̄ = (X1 + X2+…+ Xi +. …Xn)/n = (1/n)ΣXi

Son espérance est:

E(X̄) = E((1/n)ΣXi) = (1/n)ΣE(Xi) = (1/n)n μ = μ

E(X̄) = μ_X̄ = μ

Avec V(Xi) = σ², sa variance est:

V(X̄)= V((1/n)ΣXi) = (1/n²)V(Σ(Xi)) =

(1/n²) ΣV(Xi) = (1/n²) n σ² = σ²/n

V(X̄) = σ²_X̄ = σ²/n

3. Exemple

On sait que le taux de jus d'orange dans une population d'orange est de 100 mL/orange et d'écart type est de 10 mL/orange.

On préleve 16 oranges comme échantillon.

La loi de probabilité de la variable aléatoire X sur la population d'oranges est N(μ, σ) = N(100,10).

La loi de probabilité de la variable aléatoire X̄, moyenne des 16 variables aléatoires X est N(μ, σ/√16) = N(100,10/4) = N(100,2.5)

Le taux de jus d'orange reste 100 mL/orange, mais l'écart type est réduit d'un quart pour l'échatillon.

4. Convergence

La variable centrée réduite Z qu'on construit construite pour X̄ converge vers différentes lois de probabilité selon la nature de la variable aléatoire continue X, de la taille de l’échantillon n et de la connaissance que nous avons sur le paramètre σ².




1. La variance σ² est connue et n grand (n ≥ 30), on se trouve dans les conditions du théorème central limite. La loi suivie par :

(X̄ - μ)/(σ/√n) → la normale réduite: N(0,1)

Ceci reste vrai lorsque n ≤ 30 seulement si la loi suivie par X suit une loi normale.

2. La variance σ² n’est pas connue et X suit une loi normale, la loi suivie par la variable centrée réduite (X̄ - μ)/(σ̂/√n) → la loi de Student T_{n - 1} de dll = n-1.

Lorsque n ≥ 30, la loi de student tend vers une loi normale réduite

3. La variance σ² n’est pas connue et X ne suit pas une loi normale, la loi suivie par (X̄ - μ)/(σ̂/√n) n'est pas connue.

5. Loi de probabilité d’une fréquence

Dans une population il y a une proportion p des individus qui présentent une certaine propriété.

Pour un échantillon de taille n prélevé, il y a k1 éléments qui présentant cette propriété.

Dans un autre échantillon, on trouve k2 éléments qui présentant cette propriété.

L'ensemble des ki de différents échantillons est une variable aléatoire K qui suit une loi binomiale B(n, p) d'espérence E(K) = np et de variance V(K) = np(1 - p).

On construit la variable aléatoire des fréquenses F = K/n. Elle a pour:

- Espérence E(F) = (1/n) E(K) = np/n = p et pour

- Variance V(F) = (1/n²) V(K) = np(1 - p)/n² = p(1 - p)/n