Mathématiques 2: Statistiques : Médiane & quartiles

Comme la moyenne et le mode, la médiane fait partie des mesures de tendance centrale.

De plus, la médiane et les quartiles sont des mesures de position.

1. Médiane

1.1. Définition

Tout d'abord, il faut ranger la série dans l'ordre croissant.

La médiane M d’une série statistique rangée dans l'ordre croissant est la valeur de cette série qui partage la population étudiée en deux parties de même effectif chacun tels que :

– Tous les éléments du premier groupe ont des valeurs inférieures ou égales à M ;
– Tous les éléments du deuxième groupe ont des valeurs supérieures ou égales à M.

Le critère utilisé pour trouver la médiane est un critère de position; c'est à dire que c'est la position de l'effectif dans la série qui détérmine la valeur du caractère statistique.

Pour calculer la médiane d'une série statistique, il faut distinguer deux cas :

Premier cas :
Si l'effectif total N de la série est impair, La médiane M est la valeur située à la position (N + 1)/2.

Deuxième cas :
Si l'effectif total N de la série est pair, La médiane est égale à la demi somme des valeurs qui correspondent à N/2 et (N/2) + 1.

1.2. Exemples

1. Soit la série statistique suivante:

3, 5, 7, 9, 11, 13, 15, 17, 19, 21, 23.

Son effectif total est égal à 11. Il est impair.

On partage cet effetif en deux parties, donc (11 + 1)/2 = 6. Donc 6 est la position centrale de cette série.

On peut ecrire: 5 + 1 + 5 = 11.

Ainsi la médiane de cette série est sa sixième valeur, c'est à dire 13.

2. Soit la série statistique suivante:

3, 5, 7, 9, 11, 13, 15, 17, 19, 21, 23, 25.

Son effectif total est égal à 12. Il est pair.

On partage cet effetif en deux parties, donc 12/2 = 6. Ainsi la position centrale de cette série est comprise entre 12/2 et 12/2 + 1, c'est à dire 6 et 7.

Donc la médiane de cette série est la demi-somme des valeurs qui correspondent aux positions 6 et 7, c'est dire: (13 + 15)/2 = 14.

1.3. Déterminer la médiane à partir d’une
représentation graphique

On obtient une valeur approchée de la médiane à l’aide de la courbe polygonale des effectifs cumulés croissants (ou des fréquences cumulées) en prenant la valeur correspondant à la moitié de l’effectif total (ou à une fréquence cumulée égale à 50 %).



Un boîte contient 80 oranges. On veut peser ces oranges pour comparer leurs masses. Voici les résultats obtenus sous forme d'une série statistique:

masse d'une orage (g)	190	195	198	200	203	205	210	212
son effectif	7	8	15	20	12	9	6	3
effectif cumulé croissant	7	15	30	50	62	71	77	80

La courbe polygonale des effectifs cumulés est obtenue en joignant, par des segments, les points dont l’abscisse est un caractère (variable)de la série (ou l’extrémité d’une classe) et dont l’ordonnée est l’effectif cumulé correspondant à cette valeur.



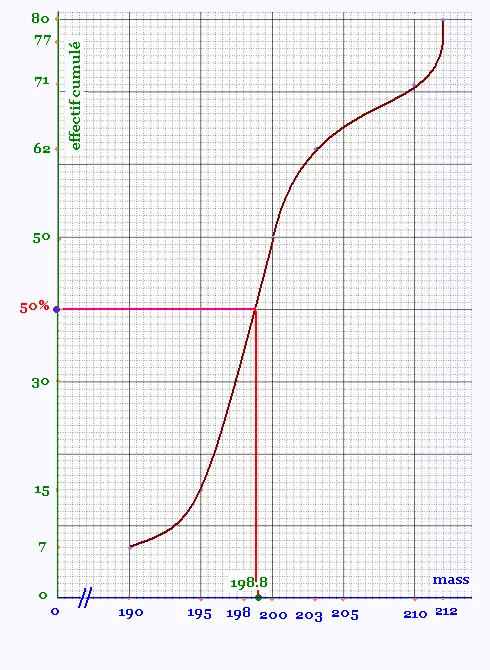
La médiane M est environ égale à 198.8 grammes. C'est à dire que la moitié de la boîte des oranges (40) pèse moins de 198.8 g ou, l'autre moitié pèse plus 198.8 g.

2. Quartiles

La médiane sépare les valeurs en deux groupes. Les quartiles les séparent en quatre groupes. Les déciles en 10, les centiles en 100, et les quantiles en n.

Si la médiane M divise la série statistique (l'ensemble des caractères) en deux parties égales, le quartile divise plutôt cette série en 4 parties égales de sorte que chaque partie représente 1/4 de l'échantillon de population.

L'ensemble des caractères est divisé en 4 parties égales, et contient donc 3 quartiles Q1, Q2 = M, et Q3.

Le quartile inférieur Q1 est la valeur du milieu de la première partie médiane, pour lequel, 25% des caractères sont inférieurs à lui et 75% lui sont supérieurs.

Le quartile supérieur Q3 est la valeur du milieu de la deuxième partie médiane, pour lequel, 75% des caractères sont inférieurs à lui et 25% lui sont supérieurs.

La différence entre le 3e quartile Q3 et le 1er quartile Q1 s'appelle écart interquartile. Cet écart s'étend sur 50% de l'ensemble des caractères autour de la médiane.

L'intervalle semi-interquartile correspond à la moitié de écart interquartile.

Soit la série statistiques suivante:

180, 192, 202, 198, 196, 200, 188, 204, 206, 208, 194, 212, 186.

Il faut toujours d'abord ranger l'ensemble des caractères dans l'ordre ascendant, donc

180, 186, 188, 192, 194, 196, 198, 200, 202, 204, 206, 208, 212.

La série contient 13 caractères. Ainsi, la médiane M est le caractère du (13 + 1)/2 = 7ième rang qui est 198. M = Q2 = 198.

180, 186, 188, 192, 194, 196, 198, 200, 202, 204, 206, 208, 212.

La 7eme position est prise par Q2, on considère donc juste les 6 premières positions pour calculer Q1 et les 6 dernières positions pour le calcul de Q3.

La première partie (de gauche) contient donc 6 caractères. Ainsi, le quartile Q1 est la valeur du caractère dont la position est comprise entre 6/2 et 6/2 + 1; c'est à dire entre le 3ième et le 4ième rang; qui est (188 + 192)/2 = 190. Q1 = 190.

180, 186, 188, 190,192, 194, 196

La deuxième partie (de droite) contient 6 caractères. Ainsi, le quartile Q3 est la valeur du caractère dont la position est comprise entre 6/2 et 6/2 + 1; c'est à dire entre le 3ième et le 4ième rang à partir de la droite; qui est (204 + 206,)/2 = 205. Q3 = 205.

200, 202, 204,205, 206, 208, 212.

3. Calcul des quartiles

3.1. La méthode

On calcule Q1, ensuite Q3 et enfin Q2 = M .

Calcul de Q1:

On divise l'effectif total par 4 (quartile) N/4

Dans le cas ou ce mombre N/4 n'est pas un entier, on prend le nombre entier qui vient directement après lui (par exemple on remplace 4.3 par 5).

Le 1er quartile est la (N/4)e valeur de la série statistique.

Calcul de Q3:

Pour Q3 on procède de la même façon mais à partir de la fin de la série statistique .

N - N/4 qui est égal à 3N/4

Ainsi, la (3N/4)e valeur est la valeur de Q3.

Calcul de Q2:

La valeur de Q2 est la valeur de la médiane M. Q2 = M.

On rappelle que pour calculer la médiane, on distingue deux cas:

l'effectif total N est un nombre impair: La médiane est égale à la valeur qui correspond au rang (N + 1)/2

l'effectif total N est un nombre pair: La médiane est égale à la demi somme des deux valeurs qui correspondent respectivement aux rangs consécutifs N/2 et N/2 + 1.

La parité (c'est à dire pair ou impair) intervient seulement dans le calcul de la médiane M = Q2.

3.2. Exemples:

Soit la série statistique dont l'effectif total N = 10:

2.5, 4.8, 2, 5, 5, 1, 8, 9, 7, 4.

D'abord, on range la série dans l'ordre croissant, ce qi donne:

1, 2, 2.5, 4, 4.8, 5, 5, 7, 8, 9

Calcul de Q1:

N/4 = 10/4 = 2.5.
On remplace 2.5 par 3.
Donc le 1er quartile Q1 est la 3e valeur, c'est-à-dire 2.5. Q1 = 2.5

Calcul de Q3:

N - N/4 = 10 - 10/4 = 7.5.
On remplace 7.5 par 8.
Donc le 3eme quartile Q3 est la 8e valeur, c'est-à-dire 7. Q3 = 7

Calcul de Q2:

l'effectif total N = 10 est un nombre pair. Donc La médiane est égale à la demi somme des deux valeurs qui correspondent respectivement aux rangs consécutifs N/2 = 5 et N/2 + 1 = 6, c'est à dire (4.8 + 5)/2 = 4.9 . Q2 = 4.9

Soit la série statistique dont l'effectif total N = 16:

2.8, 3, 2, 5, 5.5, 1.5, 8, 10, 7, 4, 6, 6, 2.2, 8.4, 9, 12.

D'abord, on range la série dans l'ordre croissant, ce qi donne:

1.5, 2, 2.2, 2.8, 3, 4, 5, 5.5, 6, 6, 7, 8, 8.4, 9, 10, 12 .

Calcul de Q1:

N/4 = 16/4 = 4.
Donc le 1er quartile Q1 est la 4e valeur, c'est-à-dire 2.8.

Q1 = 2.8

Calcul de Q3:

N - N/4 = 16 - 16/4 = 12.
Donc le 3eme quartile Q3 est la 12e valeur, c'est-à-dire 8.

Q3 = 8

Calcul de Q2:

l'effectif total N = 16 est un nombre pair. Donc La médiane est égale à la demi somme des deux valeurs qui correspondent respectivement aux rangs consécutifs 16/2 = 8 et 16/2 + 1 = 9, c'est à dire (5.5 + 6)/2 = 5.75.

Q2 = 5.75

Soit la série statistique dont l'effectif total N = 7:

10, 6, 5, 2, 8, 9, 12.

D'abord, on range la série dans l'ordre croissant, ce qi donne:

2, 5, 6, 8, 9, 10, 12.

Calcul de Q1:

N/4 = 7/4 = 1.75.
On remplace 1.75 par 2.
Donc le 1er quartile Q1 est la 2e valeur, c'est-à-dire 5.

Q1 = 5

Calcul de Q3:

N - N/4 = 7 - 7/4 = 5.25.
On remplace 5.25 par 6.
Donc le 3eme quartile Q3 est la 6e valeur, c'est-à-dire 10.

Q3 = 10

Calcul de Q2:

l'effectif total N = 7 est un nombre impair: La médiane est égale à la valeur qui correspond au rang (N + 1)/2 = (7 + 1)/2 = 4, c'est à dire 8.

Q2 = 8

4. Exercice résolu

On considère la série statistique suivante:

17, 19, 19, ..., 24, 26,..., ..., 29, 32, ..., 41, 43, ... .

• le mode est égal à 26.
• L'étendue est égale 28.
• Le quartile Q3 correspond au produit de 2 et du quartile Q1, duquel on soustrait 4.
• Le quartile Q3 est égal à la somme de 16 et du quartile Q1.

Question:

Compléter la série.

Réponse:

La série contient en tout 5 inconnues. Soit

17, 19, 19, x1, 24, 26, x2, x3, 29, 32, x4, 41, 43, x5 .

La série est déjà rangée. Son effectif total est N = 14.

a) L'étendue est la différence entre la plus grande valeur x5 et la plus petite valeur 17, soit:

x5 - 17 = 28. D'où x5 = 17 + 27 = 45

x5 = 45

b) L'effectif totale N = 14 est un nombre pair. N/2 = 7. Donc

La médiane Q2 = (Caractère(7) + Caractère(8))/2 =
(Caractère(7) + Caractère(8))/2.

On ne connait ni Caractère(7), ni Caractère(8). Ainsi la donnée de la médiane est inutile.

c)
Q3 = 2Q1 - 4       (1)
Q3 = 16 + Q1       (2)

On prend Q1 de la relation (2) et on le substitue dans la relation (1). Soit

Q1 = Q3 - 16
Q3 = 2(Q3 - 16) - 4 = 2Q3 - 32 - 4 = 2Q3 - 36. D'où
Q3 = 36

Q3 = 36

Q1 = Q3 - 16 = 36 - 16 = 20

Q1 = 20

N/4 = 14/4 = 3.5. On prend l'entier immédiatement supérieur, soit 4. Donc

Q1 = 20 = Caractère(4) = x1

x1 = 20

3N/4 = 3 x 14/4 = 10.5. On prend l'entier immédiatement supérieur, soit 11. Donc

Q3 = 36 = Caractère(11) = x4

x4 = 36

On obtient la série: 17, 19, 19, 20, 24, 26, x2, x3, 29, 32, 36, 41, 43, 45 .

d) Le seul caractère pondéré est 19 d'effectif 2. On sait que le mode est égal à 26. Donc son effectif doit être au moins égal à 3. Comme x2 et x3 sont les deux seules inconnues qui restent, celles-ci doivent donc être égales à 26.

La série finale est donc:

17, 19, 19, 20, 24, 26, 26, 26, 29, 32, 36, 41, 43, 45 .