Mathématiques 2
Statistiques
Rang centile d'une donnée statistique

1. Le rang centile d'une donnée

1. Définition

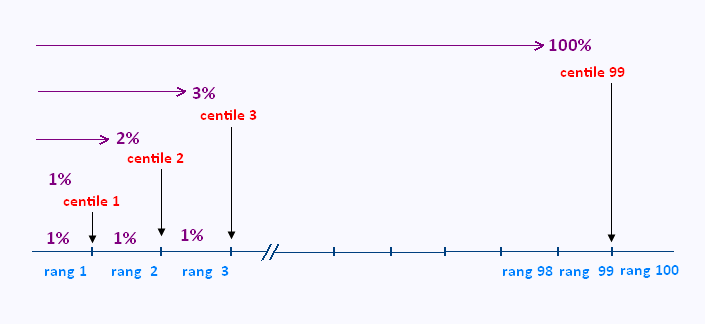
Dans une série statistique, le rang centile d'une donnée indique le pourcentage des données ayant une valeur inférieure ou égale à cette donnée.

On note que:

• Les données de même valeur doivent se retrouver dans le même rang.
• Les données les plus faibles se retrouvent dans le rang 1.
• Les données les plus élevées se retrouvent dans le rang 100.

• Si le rang centile n'est pas un entier, on l'arrondit à l'entier supérieur.



• La série étudiée doit être ordonnée. Géréralement, elle est ordonnée dans le sens croissant.

Plus la donnée considérée a une valeur élevée , plus le rang centile est élevé. C'est le cas du classemnt selon les notes obtenues par des élèves.

Plus la donnée considérée est meilleure ou performante , plus le rang centile est élevé. C'est le cas du classemnt des athlètes selon les temps mis pour parcourir une distance.

Le calcul du rang centile se fait selon le sens du meilleur ou du performant.

2. Exemples

On considère la suite statistique suivante:

5,12, 14, 17, 20, 23, 23, 44, 55,	67, 67, 67,	68, 72, 72, 78, 99, 122, 187 .
--------- 9 données -----------		------- 7 données --------

L'effectif total de la série statistique est égal à 19; c'est à dire, nous avons 19 données au total.

1. À quel rang centile appartient la donnée 44 ?

On se positionne sur la donnée 44. Il y a donc 8 données de valeur inférieure ou égale à 44.

Le pourcentage des données de valeur inférieure ou égale à 44 est : 8/19 = 0.42 = 42%.

Le rang centile de la donnée 44 est égal à 42.


2. À quel rang centile appartient la donnée 67 ?

On se positionne à partir du premier 67. Il y a donc 9 données de valeur inférieure à 67.

Le pourcentage des données de valeur inférieure à 67 est : 9/19 = 0.47 = 47%.

Le nombre de données de même valeur que 67 est égal à 3 . Sa moitié est égal à 3/2 = 1.5. Son pourcentage est égal à 1.5/19 = 0.079 = 7.9%.

Le pourcentage des données de valeur égale à 67 est 7.9%.

Le pourcentage des données de valeur inférieure ou égale à 67 est : 47% + 7.9% = 54.89% = 55%

Le rang centile de la donnée 67 est égal à 55.

3. Formule générale

Dans le cas où il ya peu de données de même valeurs, on utilse souvent a formule simple suivnate:

2. Exercices résolus

Exercice 1

Corto est le 4ième coureur le plus rapide dans une course de 500 mètres, qui compte 15 participants.

Deux autres coureurs ont le même score que lui.

Quelle est le rang centile de Corto?

On place les scores dans l'ordre croissant du mérite qui est l'ordre décroissant du temps mis à parcourir.

Corto, aisi que les deux autres, se situe au 15 - 3 = 12ième rang dans la liste:

15, 14, 13, 12, 11, 10, 9, 8, 7, 4, 4, 4, 3, 2, 1

Pour trouver le rang centile de Corto, on se place au début de la série de 4 scores identiques. Donc, il y aura 9 scores inférieures à celui de Corto :

R100 :Corto = 100 (9 + 3/2)/15 = 70

Donc, il y a 70% d’athlètes de scores égales ou inférieures à celui de Corto. Il y a 30% d’athlètes qui sont plus rapide que Corto.

Exercice 2

Voici une liste des temps en minutes mis par des cyclistes lors d'une course de vélo sur une distance de 13 km, commençant par le neilleur et se terminant par le pire.

44, 51, 55, ..., 62,	65, 65, 65,	68, ..., 85, 87
24 temps		96 temps

Quel est le rang centile des cyclistes qui ont fini en 65 minutes ?

Les meilleurs on un rang centile élevé. Donc, dans le sens de droite à gauche, il ya 96 + 3 = 99 temps après le premier 65. Le rang centile est donc:

R100 = 100 x 96 / (24 + 3 + 96) = 80.48

Les cyclistes avec un temps de 65 minutes se classent dans le 81ème rang centile.

Exercice 3

On peut aussi, dans une distribution, trouver une donnée correspond un certain rang centile. On utilise la formule suivante :

Donnée = rang centile x nombre total de données /100

Si la donnée obtenue n’est pas un nombre entier, on arrondit à l'entier inférieur.

Calculer la donnée de rang centile 56 dans la distribution suivante:

44, 51, 55, ..., 62,	65, 65, 65,	68, ..., 85, 87
24 temps		96 temps

Donnée = 56 x 123/100 = 68.88

La donnée cherchée est 68.

Exercice

Voici les scores en minutes d'une course d'endurance. Betty et Irena sont deux athlètes qui font partie de l'épreuve.

51, 53, 57, 62, 62, 65, 65, 67, 69, 70, 70 70, 75, 75, 79, 79, 80, 81, 81, 86, 86, 89, 97, 98.

les meilleurs sont les plus résistants. Nous avons les informations suivantes :

• Le rang centile du score de Betty est plus grand que son score
• Le rang cinquième du score d'irena est de un plus grand que le rang cinquième du score de Betty
• Aucun autre athlète n'a eu le même score qu'Irena
• Le score de Betty est un nombre nombre impair.

Quels sont les scores de Betty ey d'Irena ?

Réponse

L'effectif total est 24

24/5 = 4.8 , donc environ 5 groupes

51, 53, 57, 62, 62,
65, 65, 67, 69,
70, 70 70, 75, 75,
79, 79, 80, 81, 81
86, 86, 89, 97, 98.

Le rang centile du score de Betty est plus grand que son score. Seuls les données 86, 89, 88 conviennent.
Cette donnée doit être impair. Donc c'est 89


Le score de Betty est au premier rang cinquième.
Donc celui du score d'Iréna est au deuxième rang cinquième:
79, 79, 80, 81, 81


Aucun autre athlète n'a eu le même score qu'Irena. Donc c'est 80.

Le score de Betty est 89. Celui d'Iréna est 80.