Statistiques
Statistiques
descriptives
Échantillonage
Éstimation
Statistiques
inférentielles
Statistiques
Calculateurs
© The scientific sentence. 2010
|
Mathématiques 2: Statistiques:
Statistiques à deux variables
Regression linéaire
La méthode médiane-médiane
1. La méthode médiane-médiane
On procède selon les étapes suivantes:
• On ordonne les points dans l'ordre croissant des abscisses,
• on forme trois groupes de points égaux, avec
un même nombre de points dans le premier groupe et dans
le troisième groupe.
• Pour chacun des groupes, on repère les trois points médians.
On note l'abscisse médiane et l'ordonnée médiane
pour former les trois points
M1(x1, y1), M2(x2, y2), M3(x3, y3).
• On utilise les points M1 et M3 pour calculer la
pente de la droite: a = (y3 - y1)/(x3 - x1),
• On calcule la moyenne les abscisses et la moyenne des ordonnées
de ces point M1, M2, et M3 pour former le point P.
• On fait passer la droite par le point P pour calculer
l'ordonnée à l'origine b,
• On ecrit l'équation de la droite de regression avec une certaine
marge d'erreur:
y = a x + b
2. Exemple
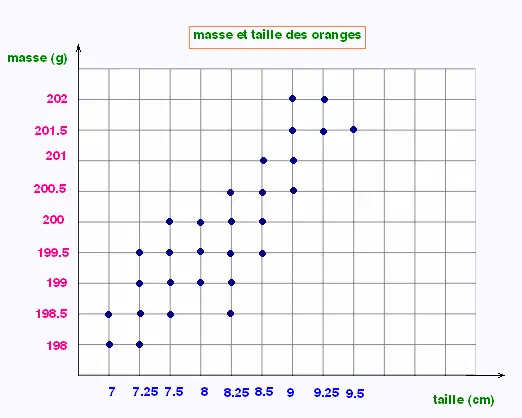
Pour l'exemple des oranges, points ordonnées en ordre
croissants des abscisses, on a:
|
| |
|
|
(7, 198) | |
(7, 198.5)
|
|
(7.25, 198) | |
(7.25, 198.5) | |
(7.25, 199) | |
(7.25, 199.5) |
|
(7.5, 198.5) | |
(7.5, 199) | |
(7.5, 199.5) |
|
| |
|
|
|
| |
(7.5, 200) |
|
(8, 199) | |
(8, 199.5) | |
(8, 200) |
|
(8.25, 198.5) | |
(8.25, 199) | |
(8.25, 199.5) | |
(8.25, 200) | |
(8.25, 200.5) |
|
(8.5, 199.5) | |
(8.5, 200) |
|
| |
|
(8.5, 200.5) | |
(8.5, 201) |
|
(9, 200.5) | |
(9, 201) | |
(9, 201.5) | |
(9, 202) |
|
(9.25, 201.5) | |
(9.25, 202) |
|
(9.50, 198) |
| |
|
Nous avons on tout 29 points. Ainsi
29 = 3 x 9 + 2 . Les 2 points qui restent
doivent être dans le deuxième groupe.
On a les points médianes suivants:
M1(7.25, 199),
M2(8.25, 199),
M3(9, 201.5).
a = (201.5 - 199)/(9 - 7.25) = 1.43
P((7.25 + 8.25 + 9)/3, (199 + 199 + 201.5)/3) = (8.17, 199.83)
y = 1.43 x + b
199.83 = 1.43 x 8.17 + b. Donc
b = 188.15
L'équation cherchée s'ecrit:
y = 1.43 x + 188.5
|
|