Statistiques
Statistiques
descriptives
Échantillonage
Éstimation
Statistiques
inférentielles
Statistiques
Calculateurs
© The scientific sentence. 2010
|
Mathématiques 2: Statistiques
Espérance et Variance
1. Loi de probabilité
Une loi de probabilité associe une probabilité à chaque valeur de la variable aléatoire.
Xi → Pi
La variable aléatoire peut être discrète ou continue lorsque
ses valeurs se trouvent dans un ensemble de valeurs ou intervalles.
La variable aléatoire utile en statistiques est la fonction qui donne les valeurs centrales comme la moyenne, la médiane ou le mode, les dispersions comme la variance ou l’écart-type et les formes de dispersion comme les fréquences absolues, relatives ou cumulées.
2. Espérance mathématique
L’espérance d’une variable aléatoire X, notée E(X)
correspond à la moyenne des valeurs possibles de X pondérées par
les probabilités qui sont associées à ces valeurs.
L’espérance est un paramètre de position qui correspond au moment d’ordre 1 de la variable aléatoire X. C’est l’équivalent de la moyenne arithmétique x̄ .
Lorsque le nombre d’épreuves N devient grand, x̄ tend vers E(X) .
2.1. Variables aléatoires discrètes
Si X est une variable aléatoire discrète définie sur
un univers probabilisé Ω, on appelle espérance de X,
le nombre réel défini par :
E(X) = Σ X(ω)P(ω) , avec
ω  Ω Ω
L’espérance mathématique est également notée
μ(X), μXX ou encore μ.
On donne une autre définition de l’espérance
d’une variable aléatoire discrète X:
À ω Ω, on associe l’image x de ω
telle que X(ω) = x et P(x) = p. Ω, on associe l’image x de ω
telle que X(ω) = x et P(x) = p.
Si X est une variable aléatoire discrète de loi
de probabilité (xi, pi) définit sur un nombre fini
N d’évènements élémentaires alors :
E(X) = Σ xipi
i: 1 → N.
2.2. Variables aléatoires continues
Si X est une variable aléatoire absolument continue
de densité de probabilité ƒ, on appelle
espérance de X, le réel E(X) , défini par:
E(X) = ∫ x ƒ(x)dx
x: - ∞ → + ∞
Cette intégrale doit être convergente.
2.3. Propriétés de l’espérance
Les propriétés de l’espérance restent
valables pour une variable aléatoire discrète
ou une variable aléatoire absolument continue.
Si X et Y sont deux variables aléatoires
définies sur un même univers Ω, admettant
une espérance, alors :
(P1): E(X + Y) = E(X) + E(Y)
(P2): E(aX) = aE(X) 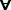 a a  R R
(P3): Si X ≥ 0 alors E(X) ≥ 0
(P4): Si X est un caractère constant tel que :
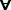 ω ω Ω
X (ω) = k Ω
X (ω) = k
alors E(X) = k
On démontre ces propriétés dans le cas
de deux variables aléatoires discrètes avec pi,
la probabilité (équiprobabilité) de réalisation
de {X = xi} et {Y = yi} et N évènements
élémentaires.
(P1): E(X + Y) = Σ (xipi +
yipi) =
Σ xipi +
Σ yipi = E(X) + E(Y)
(P2): E(aX) = Σ (axipi ) =
a Σ xipi = a E(X)
(P3): X ≥ 0 veut dire tous les xi sont
positifs ou 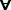 ω ω Ω X (w) ≥ 0. Ω X (w) ≥ 0.
Comme une probabilité pi est toujours positive; celà
implique E(X) ≥ 0.
(P4): E(X)= Σ kpi =
k Σ pi = k; puisque Σ pi = 1.
3. Variance
La variance V(X) d’une variable aléatoire X
est l’espérance mathématique du carré de l’écart de X
à son espérance mathématique.
C’est un paramètre de dispersion qui correspond au
moment centré d’ordre 2 de la variable aléatoire X.
C’est l’équivalent de la variance observée S2.
Lorsque le nombre d’épreuves N est grand, S2
tend vers V(X).
Si X est une variable aléatoire ayant une espérance
E(X), on appelle variance de X le nombre réel :
V(X) = E([X - E(X)]2)
Avec une autre notation:
V(X) = E([X - E(X)]2) =
E(X2 – 2XE(X) + [E(X)]2) =
E(X2) – 2E[XE(X)] + E[[E(X)]2]
Avec la Propriété P1 de l’espérance, on a:
V(X) = E(X2) – 2[E(X)]2 +
E[[E(X)]2] =
E(X2) – 2[E(X)]2 +
E[[E(X)]2]
Avec la Propriété P4 de l’espérance
([E(X)]2 est constant), on a:
V(X) = E(X2) – 2[E(X)]2 +
[E(X)]2 =
E(X2) – [E(X)]2
V(X) = E(X2) – [E(X)]2
Une variance est toujours positive.
La variance est également notée σ2.
Si X est une variable aléatoire ayant
une variance V(X), on appelle écart-type de X,
le réel racine carrée de la variance:
σ(X) = √[V(X)]
3. 1. Variables aléatoires discrètes
Si X est une variable aléatoire discrète
de loi de probabilité (xi, pi) définie sur un nombre
fini N d’évènements élémentaires, alors la variance
est égale à :
V(X) = E(X2) – [E(X)]2 =
Σ i:1N xi2pi –
[Σ i:1N xipi]2
V(X) =
Σ i:1N xi2pi –
[Σ i:1N xipi]2
3.2. Variables aléatoires continues
Si X est une variable aléatoire continue donnée par
sa densité de probabilité ƒ alors la variance de
X est le nombre réel positif tel que :
V(X) = ∫ (x - E(X))2 f(x) dx =
∫ x2f(x) dx - (E(X))2)
x: - ∞ → +∞.
3.3. Propriétés de la variance
Si X est une variable aléatoire admettant
une variance alors :
(P1) 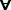 a a  R, V(aX) = a2 V (X) R, V(aX) = a2 V (X)
(P2) 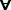 a, b a, b  R, V(aX + b) = a2 V (X) R, V(aX + b) = a2 V (X)
(P3) V(X) = 0  X = E(X) X = E(X)
|
|