Mathématiques
45
Théorème de Thalès
et sa réciproque
© The scientific sentence. 2010
|
Mathématiques 45: Géométrie
Théorème de Thalès
Agrandissement – Réduction
1. Définitions
Agrandir, c’est multiplier toutes les dimensions d’une figure géométrique par un même nombre k > 1, en conservant la forme de la figure.
Réduire, c’est multiplier toutes les dimensions d’une figure géométrique par un même nombre k tel que 0 < k < 1, en conservant la forme de la figure.
Si deux figures ont une même forme et des longueurs proportionnelles, alors l’une est un agrandissement ou une réduction de l’autre.
2. Propriétés:
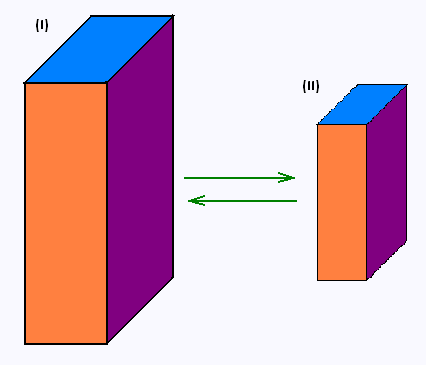
• dans un agrandissement ou une réduction, les angles, la perpendicularité et le parallélisme sont conservés.
• si on peut multiplier les dimensions par k (≠ 0)
dans un sens, alors on peut les diviser par k pour revenir à
la figure initiale.
• Si k est le coefficient de proportionnalité des longueurs
de la figure (I) à la figure (II), alors :
- Si k > 1, la figure (II) est un agrandissement de la figure (I),
- Si 0 < k < 1, la figure (II) est une réduction de la figure (I),
- Si k = 1, la figure (II) est une reproduction exacte de la figure (I).
• si k est le coefficient de proportionnalité des longeurs, alors:
k est le coefficient de proportionnalité du périmètre,
k2 est le coefficient de proportionnalité d'aire ,
k3 est le coefficient de proportionnalité du volume.
3. Exercice
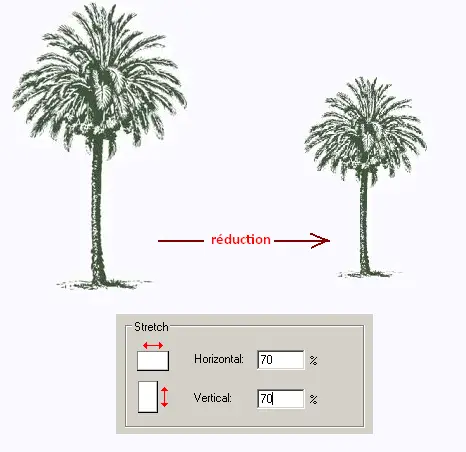
a) Quel est le coefficient utilisé pour la réduction de cette image
réalisée sur le PaintBrush de Microsoft.
b) En déduire le coefficient d'aggrandissement qui lui correspond.
c) Si on réduit l'image obtenue une deuxième fois de 30%, quelle serait la valeur du nouveau coefficient de réduction ?
4. Cas particuler: les rapports de Thalès
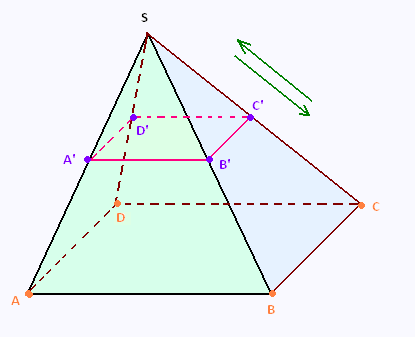
Le théorème de Thalès et par conséquent les rapports de Thalès
sont un cas particuler des transformations d'agrandissement et de
réduction qui se font sur des triangles.
L'agrandissement ou la réduction d'un objet à n triangles impliquent
n x 3 rapports de Thalès.
Pour cet exemple d'une pyramide droite à base rectangulaire,
la transfornmation de'agrandissement ou de réduction implique
4 x 3 rapports de Thalès.
5. Autre exercice
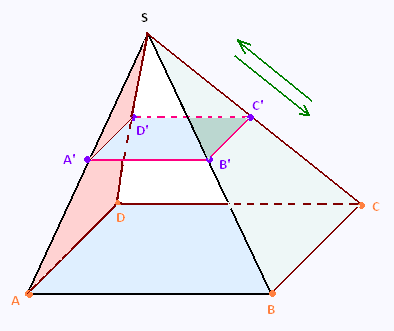
a) Ecrire les 4 triplets de rapports de Thalès pour cette
pyramide.
On suppose que la pyramide est un tétraèdre (ou pyramide
régulière à base carrée, donc 8 arêtes isométriques), et
que le coefficient de transformation (ou de proportionnalité)
est égal à 1/2.
Une arête du tétraèdre mesure 10 cm.
b) Calculer le périmètre de la grande base et en déduire
celui de la petite base trnasformée de la première.
c) Calculer l'apothème latéral a1 et l'apothème
de base a2.
d) Calculer l'aire latérale de la grande pyramide.
En déduire celle de la petite.
e) Calculer la hauteur de la grande pyramide.
f) Calculer le volume de la grande pyramide.
En déduire celui de la petite.
N.B. Le volume de la pyramide est égal au tiers du produit
de l'aire de la base par la hauteur de la pyramide.
|
|