Mathématiques 23 : Géométrie
Théorème de Thalès
Estimation de la hauteur d'un arbre

Estimation de la hauteur d'un arbre au
moyen de la croix du bûcheron

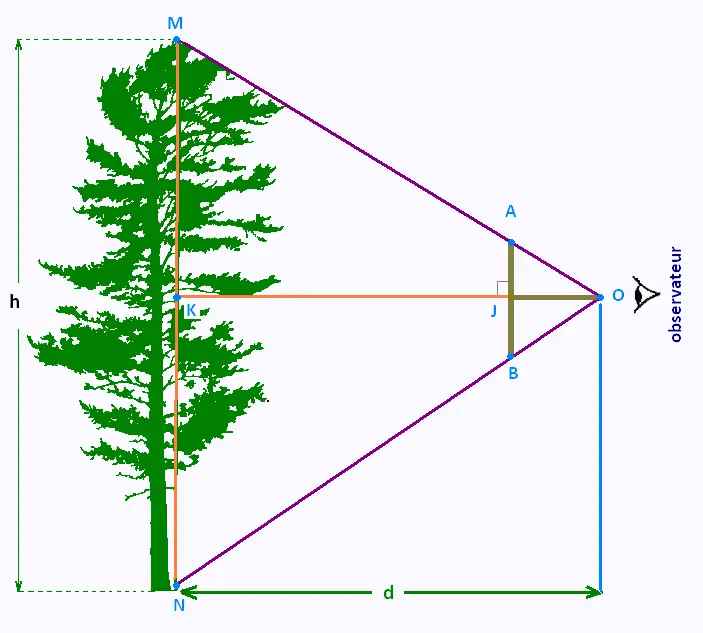
Nous allons utiliser une méthode dite de la croix du bûcheron , basée sur le théorème de Thalès, pour estimer la hauteur d'un arbre.

On peut utiliser aussi cette méthode pour estimer toute hauteur inaccessible.

Cette méthode nécessite un té formé par deux bâtons de même longueur.

On considère un arbre de hauteur NM, à une distance d de l'observateur.

On maintient la croix parallèle à l'arbre de telle sorte que (NM) est parallèle à (AB).

Dans le triangle OMN, le théorème de Thalès s'ecrit:

OA/OM = AB/NM

Dans le triangle OKM, le théorème de Thalès s'ecrit:

OJ/OK = OA/OM

D'où:

AB/NM = OJ/OK

Puisque les bâtons de la croix sont de même longueur , OJ = AB.

Puisque [O,K] est perpendiculaire à [M, N] , et que l'observateur se tient verticalement, alors OK = d.

Il vient donc:

AB/NM = AB/d . D'où: MN = d .

h = d

Avec la croix du bûcheron, la hauteur de l'arbre est égale à la distance de cet arbre à l'observateur.