Mathématiques 45: Théorème de Thalès direct

Applications

1. Hauteur de la pyramide

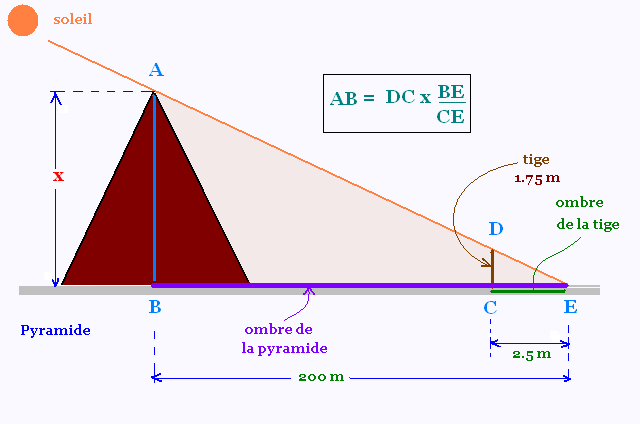
Pour mesurer la hauteur AB de la pyramide:

• on plante verticalement une tige CD de longeur 1.75 m,
• Sur le sol, on mesure l'ombre CE de cette tige: CE 2.5 m,
• Ensuite, on mesure l'ombre BE de la Pyramide: BE = 200 m.

E étant le point de rencontre des deux ombres.

Les segments [AB] et [CD] sont verticaux, donc parallèles.

D'après le théorème de Thalès, on ecrit:

EC/EB = DC/AB

Il vient:

AB = EB x DC/EC

AB = EB x DC/EC = 200 x 1.75/2.5 = 140.00 m

La hauteur de la pyramide est de 140 mètres.

2. Largeur d'une rivière

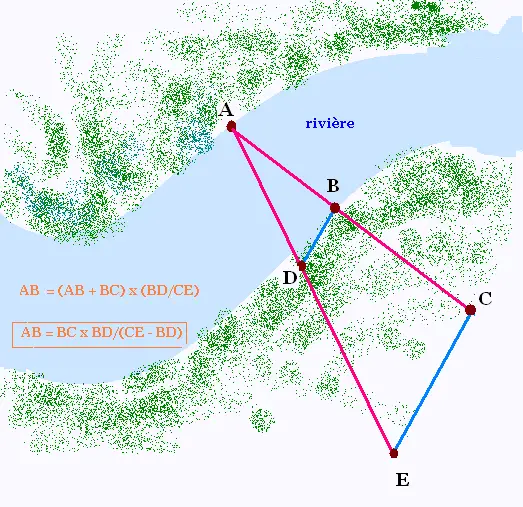
On cherche la largeur AB. On marque deux droites parallèles DB et EC. Par la vue on aligne les points A, B et C d'une part et A, D et E d'autre part.
Dans la rive où on se place on connait les mesures des segments [B,C] , [B,D] et [C,E].

Les [B,D] et [C,E] sont parallèles. D'après le théorème de Thalès, on ecrit:

AB/AC = BD/CE.
Comme AC = AB + BC, donc
AB = BC x BD/(CE - BD)

AB = BC x BD/(CE - BD)

BC = 33 m, CE = 20 m, BD = 8 m

AB = 33 x 8/(20 - 8) = 33 x 2/3 = 22 m

La largeur de la rivière est de 22 mètres.

3. Profondeur d'un puits

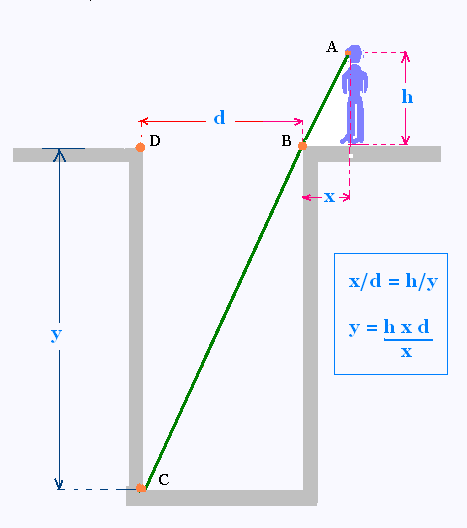
On peut utiliser les rapports de similitude pour mesurer la profondeur d'un puit.

Une personne mesurant 1.70 m de long se place à 1 m du bord du puits de 1,50 m de diamètre et regarde le coin au fond du puits.

Cette situation permet de calculer la profondeur du puits:

y = hd/x

4. Hauteur d'un arbre avec un miroir

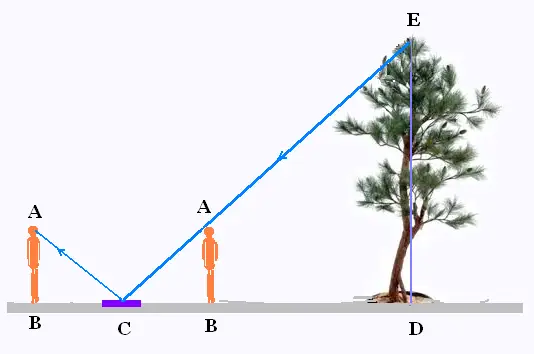
Une personne de 1.75 m de long voit le sommet d'un arbre dans un miroir placé sur le sol à 0.50 m de son pieds et à une distance de 50.00 m du pieds de l'arbre.

La personne et l'arbre sont debout perpendiculaires au sol. Le pied de la personne, le miroir et le pied de l'arbre sont alignés, c'est à dire qu'ils se trouvent le long d'une ligne droite.

C est le point sur le miroir où on voit le sommet de l'arbre.
Quelle est la hauteur de l'arbre?


Solution

Les segments [AB] et [ED] sont parallèles.

D'après le théorème de Thalès, on ecrit:

ED/AB = DC/BC

Il vient:

ED = AB x DC/BC

ED = AB x DC/BC = 1.75 x 50/0.5 = 175.00 m

La hauteur de l'arbre est de 175 mètres.

5. Hauteur d'un palmier avec caméra

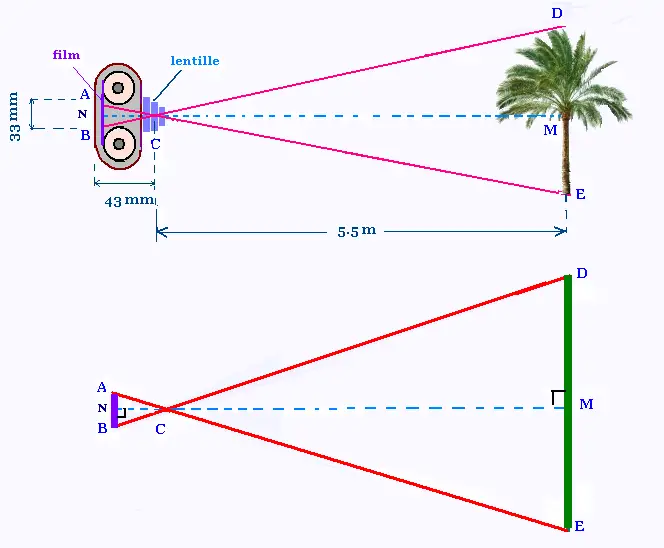
L'image d'un palmier sur le film d'une caméra est de longueur 33 mm, la distance entre la lentille de l'objectif et le film est de 43 mm et la distance entre l'objectif et le palmier est de 5.50 m.
Quelle est la hauteur du palmier photographié?

Solution

Soit DE et AB les hauteurs de l'arbre et de son image sur le film, respectivement. Le point C désigne la lentille de l'objectif.

Le distances CN et CM représentent les hauteurs des triangles ABC et DEC. M est le milieu du côté [DE] et N le milieu du côté [AB].

[AB] est parallèl à [DE]. D'après le théorème de Thalès, on ecrit:

CN/CM = AN/EM = 2AN/2EM = AB/DE

Donc DE = AB x CM/CN

DE = 0.033 x 5.5/0.043 = m

La hauteur du palmier est de 4.22 m.