Mathématiques 45: Géométrie
Théorème de Thalès
Exercices divers

Exercice résolu

Dans cet exercice, nous utiliserons le théorème des milieux, la réciproque du théorème des milieux, une propriété des droites parallèles et le théorème de Thalès direct.

Rappels:

1. Le théorème des milieux:

La droite qui passe par les milieux de deux côtés d'un triangle quelconque est parallèle au troisième côté.

La longueur du segment qui a pour extrémités les milieux de deux côtés d’un triangle quelconque est égale à la moitié de celle du troisième côté.

2. La réciproque du théorème des milieux:

Dans un triangle quelconque, si une droite passe par le milieu d’un côté parallèlement à un deuxième côté, alors cette droite coupe le troisième côté en son milieu.

3. Le théorème de Thalès:

Dans un triangle ABC,
si M est un point du côté [AB], N un point du côté [AC],
et si les droites (BC) et (MN) sont parallèles,
alors : $$\bf\color{purple}{ \dfrac{\text{AM}}{\text{AB}} = \dfrac{\text{AN}}{\text{AC}} = \dfrac{\text{MN}}{\text{BC}} }$$
4. La propriété des droites parallèles::

Si deux droites sont parallèles à une même troisième, alors elles sont parallèles entre elles.

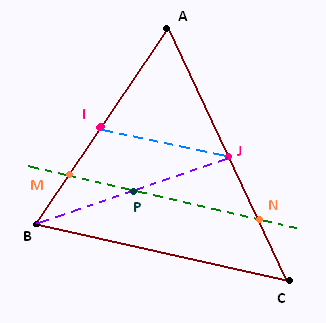
On donne:

AM/AB = 3/4 et
(MN) //(BC).

I est le milieu de [A,B] et J le milieu de [A,C].

Question:

Calculer tous les rapports de Thalès possibles.

Réponse:

D'après le théorème de Thalès:
$$\bf\color{purple}{ \dfrac{\text{AM}}{\text{AB}} = \dfrac{\text{AN}}{\text{AC}} = \dfrac{\text{MN}}{\text{BC}} = \dfrac{\text{3}}{\text{4} } }$$
I est le milieu de [A,B], donc AI = IB. Il vient donc:

$\bf\color{purple}{ \dfrac{\text{AM}}{\text{AB}} = \dfrac{\text{3}}{\text{4} } }$ donc $\bf\color{purple}{ \dfrac{\text{BM}}{\text{AB}} = \dfrac{\text{1}}{\text{4} } }$

$\bf\color{purple}{ \dfrac{\text{BM}}{\text{2 BI}} = \dfrac{\text{1}}{\text{4} } }$ donc $\bf\color{purple}{ \dfrac{\text{BM}}{\text{BI}} = \dfrac{\text{1}}{\text{2} } \\ }$

Ainsi M est le milieu de [BI].


D'autre part

$\bf\color{blue}{ \dfrac{\text{AN}}{\text{AC}} = \dfrac{\text{3}}{\text{4} } }$ donc $\bf\color{blue}{ \dfrac{\text{CN}}{\text{AC}} = \dfrac{\text{1}}{\text{4} } }$

$\bf\color{purple}{ \dfrac{\text{CN}}{\text{2 CJ}} = \dfrac{\text{1}}{\text{4} } }$ donc $\bf\color{purple}{ \dfrac{\text{CN}}{\text{CJ}} = \dfrac{\text{1}}{\text{2} } }$

Ainsi N est le milieu de [CJ] .


De plus

M est le milieu de [BI] et (MN)//(IJ).
D'aprés la réciproque du théorème des milieux pour le triangle BIJ, la droite (MN) coupe la droite (BJ) en son milieu.

Ainsi P est le milieux du côté [BJ].


D'après le théorème des milieux, on a: (IJ)// (BC).

D'après la propriété des droites parallèles,
(MN)//(BC) et (IJ)//(BC) donc (IJ)//(MN).

D'après le théorème de Thalès pour le triangle, BIJ:

$\bf\color{purple}{ \dfrac{\text{BM}}{\text{BI}} = \dfrac{\text{BP}}{\text{BJ} } = \dfrac{\text{MP}}{\text{IJ}} = \dfrac{\text{1}}{\text{2}} }$

Et pour le triangle BJC

$\bf\color{purple}{ \dfrac{\text{JP}}{\text{JB}} = \dfrac{\text{JN}}{\text{JC} } = \dfrac{\text{PN}}{\text{BC}} = \dfrac{\text{1}}{\text{2}} }$

Exercice 1

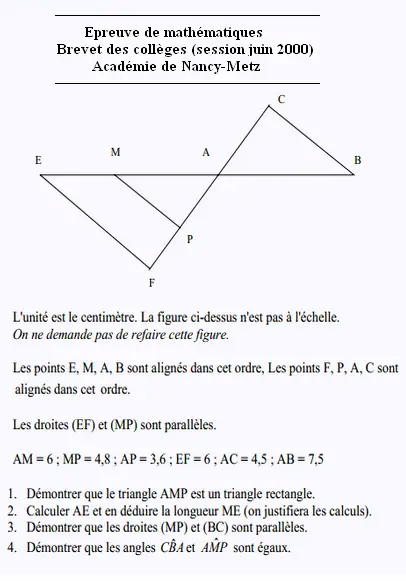
Exercice 2

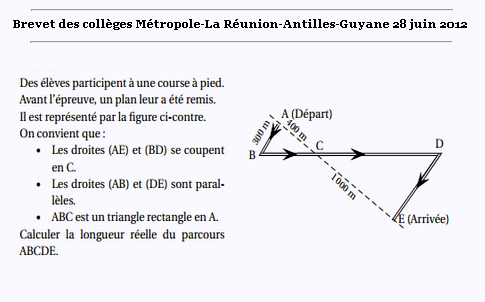
Exercice 3

Exercice 4

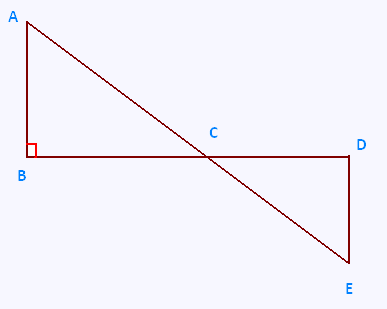
Les points A,C et E sont alignés, ainsi que les points B,C et D.

Le triangle ABC est rectangle en B.

Les longueurs suivantes sont exprimées en centimètres.

BC = 12 ; CD = 9,6 ; DE = 4 ; CE = 10,4.

1°) Montrer que le triangle CDE est rectangle en D.
2°) En déduire que les droites (AB) et (DE) sont parallèles.
3°) Calculer la longueur AB.