Mathématiques
45
Théorème de Thalès
et sa réciproque
© The scientific sentence. 2010
|
Mathématiques 45:Géométrie
Théorème de Thalès
Exercices
Exercices: Théorème de Thalès
1. Exercice résolu 1
Montrer que la configuration 2 est une configuration de Thalès.
C'est à dire qu'elle est équivalente à la configuration 1.
Les trois rapports de Thalès de la configuration 2 s'ecrivent:
En inversant ces rapports, on obtient les nouveaux rapports de Thalès, qui correspondenr à ceux de la configuration 1:
Le configurations 1 et 2 donnent les mêmes rapports. Elles sont donc équivalentes.
2. Exercice résolu 2
Montrer que la configuration 3 est une configuration de Thalès.
C'est à dire qu'elle est équivalente à la configuration 1.
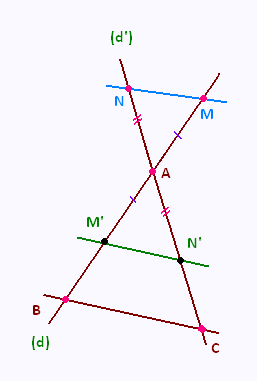
Les droites (d) et (d’) sont sécantes en A ;
B et M sont deux points de la droite (d), distincts de A ;
C et N sont deux points de la droite (d’), distincts de A ;
les droites (BC) et (MN) sont parallèles.
• Par la symétrie de centre A, on construit les points M’ et N’,
symétriques des points M et N respectivement.
Donc (M’N’) est la symétrique de (MN) par rapport à A.
Or, la symétrique d’une droite par rapport à un point est une droite qui lui est parallèle.
On en déduit que les droites (MN) et (M’N’) sont parallèles.
• De plus, on sait que les droites (MN) et (BC) sont parallèles.
Or, si deux droites sont parallèles, alors toute parallèle à l’une est parallèle à l’autre.
On en conclut que les droites (M’N’) et (BC) sont parallèles.
• M’ est le symétrique de M par rapport à A, donc AM’ = AM.
N’ est le symétrique de N par rapport à A, donc AN’ = AN.
Les segments [MN] et [M’N’] sont symétriques par rapport à A. Or,
la symétrie centrale conserve les longueurs, donc MN = M’N’.
• Dans le triangle ABC, M’ est un point du côté [AB], N’ est un point du côté [AC] et les droites (M’N’) et (BC) sont parallèles,
alors
Or, on a montré que AM’ = AM, AN’ = AN et que M’N’ = MN, donc :
Le configurations 1 et 3 donnent les mêmes rapports. Elles sont donc équivalentes.
Exercices: Réciproque du Théorème de Thalès
1. Exercice 1
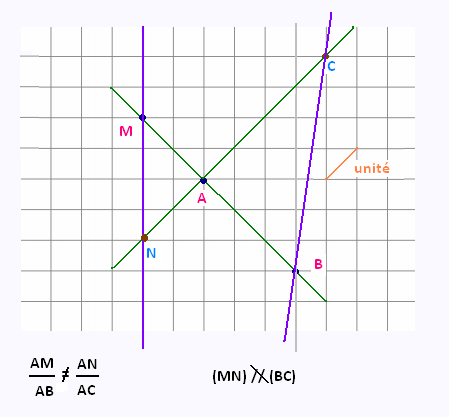
Montrer que parmi les quatres dessins suivants, un seul
correspond à une configuration de Thalès. Justifier les réponses.
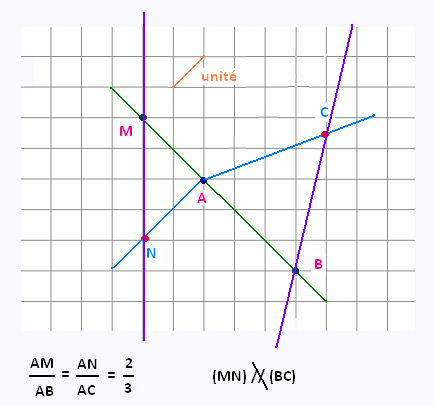
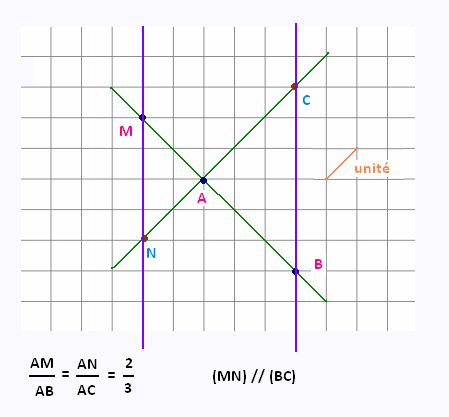
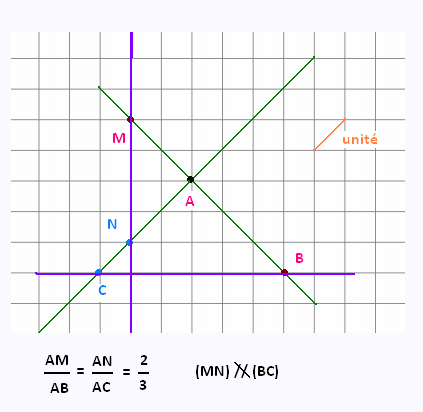
2. Exercice 2

Parie 1
Figure (a): ABC est un triangle. Le point M est un point du segment (AB),
le point N est un point de [AC], avec
Les droites (BC) et (MN) sont-elles parallèles ?
D'après le réciproque du théorème de Thalès, oui.
Parie 2
ABC est un triangle. Le point M est un point de la droite (AB),
le point N est un point de (AC), avec
Les droites (BC) et (MN) sont-elles parallèles ?
Sur le figure (b) et (b') oui. Sur le figure c): non.
La proportion donnée n'est pas suffisante. Pour que les droites (BC) et (MN) soient
parallèles, on doit avoir BAM et CAN alignés dans
cet ordre.
C'est le cas de (a), (b) et (b'), mais pas de (c).
Parie 3
Pour la figure (a), on donne:
On donne : AM = 2, AB = 3, AN = 2.5.
Calculer la mesure du côté [AC].
On ne peut pas calculer AC. Il manque une donnée. On ne peut pas
appliquer le théorème de Thales puisqu'on ne sait pas si
les droites (MN) et (BC) sont parallèles ou non.
Parie 4
Pour la figure (b'), on donne:
On donne : AB = 5, et AC = 6
Calculer la mesure du côté [AC].
Les droites (MB) et (NC) sont sécantes en A. Les droites (MN) et (BC) sont parallèles. D'après le théorème de Thalès, on a :
Pour calculer AC, Il manque une donnée qui est la valeur de AM. Les données numériques ne sont pas suffisantes pour résoudre le problème.
Parie 5
Pour une figure de type (a), on donne:
AM = 2, et AB = 6, AN = 3, et AC = 10
(MN) et (AB) sont-elles parallèles ?
Les points A, M, B d'une part et A, N, C d'autre part sont bien alignés dans le même ordre. Mais
donc
Ainsi les droites (MN) et (BC) ne sont pas parallèles.
|
|