Mathématiques
45
Théorème de Thalès
et sa réciproque
© The scientific sentence. 2010
|
Mathématiques 23 : Géométrie
Théorème de Thalès direct
Sa réciproque
Sa contraposée
Choses que j'aurais voulu qu'on me dise
lorsque j'étais jeune..
1. Logique mathématique
On rappelle, qu'en Logique mathématique, que
si deux propositions A et B vérifient l'implication :
Si A est vraie, alors B est vraie.
Dans ce cas, sa réciproque est:
Si B est vrai, alors A est vrai ou fausse.
et sa contraposée est :
Si B est fausse, alors A est fausse.
• Une implication est un théorème. C'est à dire une formule qui est toujours vraie, dont A est l'hypothèse et B la conclusion.
• La réciproque d'une implication n'est pas
nécessairement un théorème.
• La contraposée d'un théorème est toujours vraie, donc c'est aussi un théorème.
• Une implication et sa contraposée sont deux manières différentes pour affirmer une même chose.
La réciproque d'une implication est un théorème s'il est vraie.
La réciproque du théorème de Pythagore est un théorème.
La réciproque du théorème de Thalès est un théorème.
2. Théorème de Thalès direct
Voici le théorème de Thalès direct:
Si les points A, M, B et A, N, C sont alignés dans cet ordre, et
Si (MN) est parallèle à (BC),
Alors
Ce théorème nécessite donc deux triplets de points (A, B, M) et
(A, N, C), alignés dans cet ordre, ayant un point commun A, formant deux droites parallèles (MN) et (BC).
• Voici des conditions où les droites (MN) et (BC) sont parallèles, et où les triplets de points (A, B, M) et (A, N, C) ne sont pas alignés.
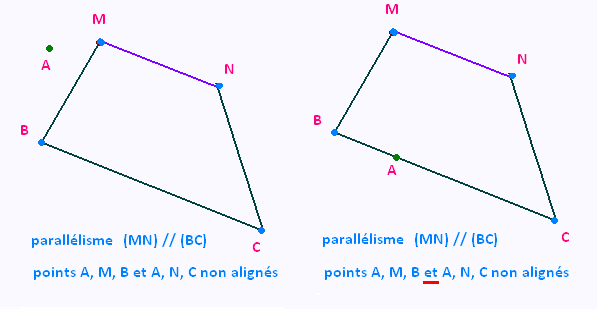
Ces condions ne se prêtent pas au théorème de Thalès.
• Voici des conditions où les droites (MN) et (BC) sont parallèles, et où les triplets de points (A, B, M) et (A, N, C)
sont alignés, mais pas dans cet ordre.
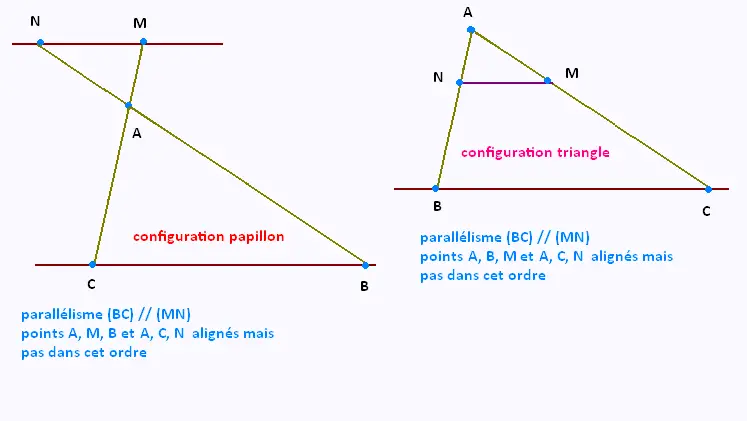
Ces condions ne se prêtent pas au théorème de Thalès.
• Voici des conditions où les droites (MN) et (BC) ne sont pas parallèles, et où les triplets de points (A, B, M) et (A, N, C)
sont alignés, et dans cet ordre.
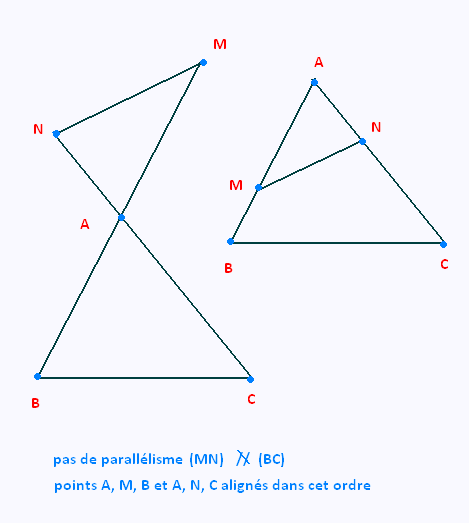
Ces condions ne se prêtent pas au théorème de Thalès.
• Voici des conditions où les droites (MN) et (BC) sont parallèles, et où les triplets de points (A, B, M) et (A, N, C)
sont alignés, et dans cet ordre.
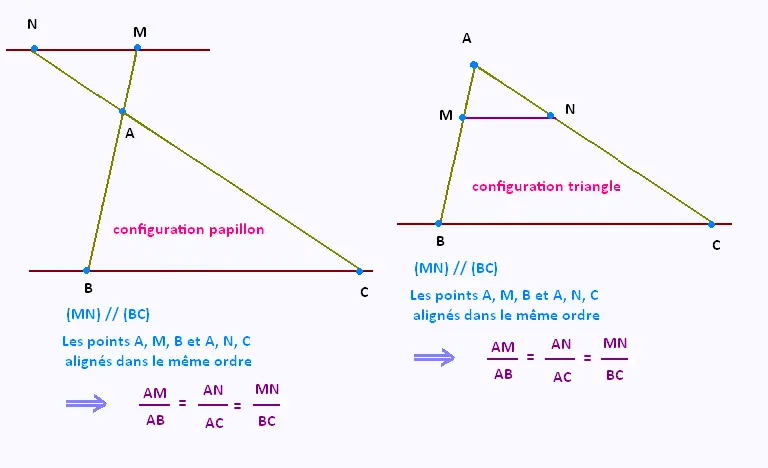
Ce sont ces condions qui sont les préalables au théorème de Thalès.
Pour que les droites (MN) et (BC) soient parallèles, et
les triplets de points (A, B, M) et (A, N, C) soient alignés, et dans cet ordre, il n'existe que ces deux configurations. Une
est dite configuration triangle, l'autre
configuration papillon.
Méthode pour utiliser le théorème de Thalès direct:
• on s'assure de l'alignement des points,
• on s'assure du parallélisme des droites relatives,
• on applique le théorème.
3. Réciproque du théorème de Thalès
Voici la réciproque du théorème de Thalès:
Si A,M,B et A,N,C sont alignés dans le même ordre ET si ,
,
alors les droites (MN) et (BC) sont parallèles.
On note qu'il faut considérer DEUX conditions, et
qu'il suffit d'une seule proportion.
La réciproque du théorème de Thalès permet de prouver que
deux droites sont parallèles.
La méthode:
Méthode pour utiliser le théorème de Thalès
réciproque:
• on s'assure de l'alignement des points,
• on calcule séparément les deux rapports,
• on compare les deux résultats.
• on conclut positivement.
- Si les points sont alignés dans l'ordre ET:
• Si les deux rapports sont égaux, les doites sont parallèles.
• Si les deux rapports sont différents, les doites ne sont pas parallèles.
• Si les deux rapports sont à peu près égaux, on ne peut pas conclure.
- Si les points ne sont pas alignés dans l'ordre, les doites ne sont pas parallèles.
Exemple 1:
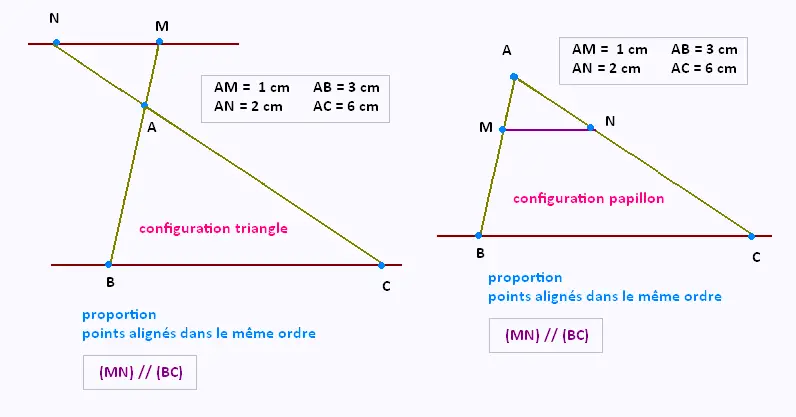
• On sait que les pints A, M, B et A, N,C sont alignés dans le
même ordre,
De plus, on sait que AB = 3 cm, AM = 1 cm, AN = 2 cm, et AC = 6 cm.
•
, .
D'où :
D'après la réciproque du théorème de Thalès, (MN)// (BC).
• Les droites (MN) et (BC) sont parallèles.
Exemple 2:
• Voici des conditions où l'on a la proportion:
, et où les triplets de points (A, B, M) et (A, N, C)
ne sont alignés.
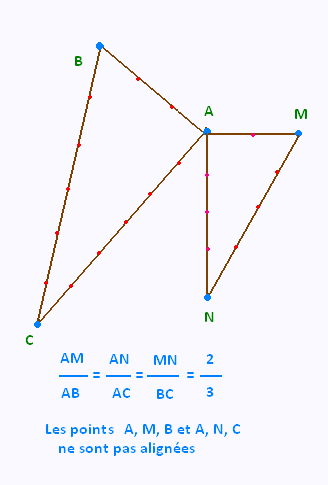
Ces condions ne se prêtent pas au théorème de Thalès réciproque.
Exemple 3:
• Voici des conditions où l'on a la proportion:
, et où les triplets de points (A, B, M) et (A, N, C)
ne sont alignés dans cet ordre.
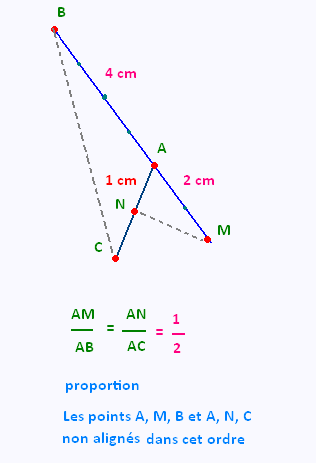
Ces conditions ne se prêtent pas au théorème de Thalès réciproque.
Les conditions sur l'alignement et la proportion qui ne se prêtent pas au théorème de Thalès réciproque font l'objet
de sa contraposé.
4. Contraposée du théorème de Thalès
La propriété contraposée du théorème de Thalès permet de prouver que deux droites ne sont pas parallèles.
Méthode pour utiliser la contraposée du théorème de Thalès :
• on s'assure de l'alignement des points,
• on calcule séparément les deux rapports,
• on compare les deux résultats.
• on conclut négativement.
Voici la contraposée du théorème de Thalès;
Si •
alors (MN) et (BC) ne sont pas parallèles.
OU si
A, M, B et A, N, C ne sont pas alignés dans le même ordre,
alors (MN) et (BC) ne sont pas parallèles.
Une condition suffit.
Exemple 1:
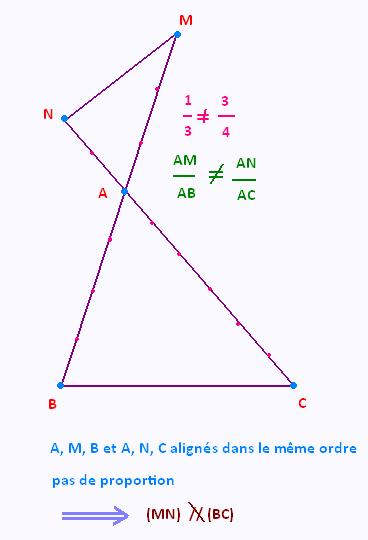
alors (MN) et (BC) ne sont pas parallèles.
Exemple 2:
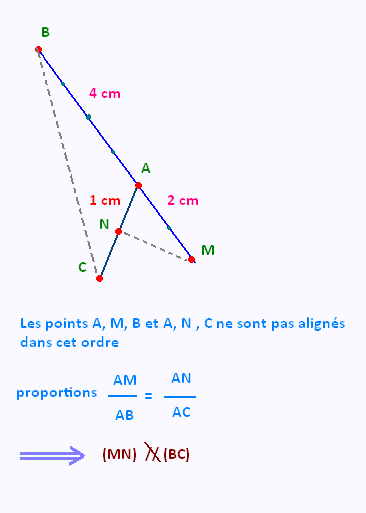
A, M, B et A, N, C ne sont pas alignés dans le même ordre,
alors (MN) et (BC) ne sont pas parallèles.
5. Théorème de Thalès: Résumé
• Théorème de Thalès direct:
Si les points A, M, B et A, N, C sont alignés dans cet ordre, et
Si (MN) est parallèle à (BC),
Alors
• Réciproque du théorème de Thalès:
Si A,M,B et A,N,C sont alignés dans le même ordre ET si ,
,
alors les droites (MN) et (BC) sont parallèles.
• Contraposée du théorème de Thalès;
• Si
alors (MN) et (BC) ne sont pas parallèles.
ou
• Si
A, M, B et A, N, C ne sont pas alignés dans le même ordre,
alors (MN) et (BC) ne sont pas parallèles.
|
|