Mathématiques
45
Théorème de Thalès
et sa réciproque
© The scientific sentence. 2010
|
Mathématiques 45: Géométrie:
Triangles isométriques
Théorème de Pythagore
Théorème de Thalès
Exercice 1 :
Données:
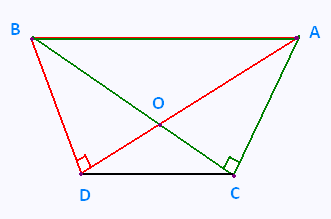
Les triangles ABC et ADB sont rectangles et isométriques.
Leurs cathètes mesurent respectivement 40 cm et 80 cm.
On demande la longueur du segment [D,C].
Réponse
•
On sait que les triangles ABC et ADB sont rectangles en
C et D respectivement et sont isométriques.
De plus, AD = BC = 80 cm et BD = AC = 40 cm.
•
D'après la propriété de Pythagore,
Dans le triangle ABC, AB2 = AC2 +
BC2. Soit:
AB2 = 402 + 802 =
402 + (2 x 40)2 =
402 + 4 x 402 = 5 x 402.
D'où:
AB = 40√5
AB = 40√5 cm
Puisque les triangles ABC et ADB sont isométriques,
mes(CBA) = mes(DAB), et donc le triangle OAB est isocèle.
D'où OA = OB .
OA = OB
Puisque AD = BC et OA = OB, alors OC = OD et donc le triangle ODC est isocèle. D'où:
mes(ADC) = mes(DCB).
Il vient donc:
mes(CBA) + mes(DAB) = mes (O) - 180o =
mes(ADC) + mes(DCB).
Qui se réduit à :
2 mes(CBA) = 2 mes(DCB). On obtient:
mes(CBA) = mes(DCB)
Ces deux angles alternes internes sont isométriques. Donc
Les droites (AB) et (DC) sont parallèles.
Les droites (AB) et (DC) sont parallèles.
Les point O, C, B et O, D, A sont alignées dans cet ordre,
de plus (AB) // (DC); la propriété
de Thalès s'ecrit alors:
OC/OB = OD/OA = DC/AB
Nous avons :
OA = AD - OD
Le trangle AOC est rectangle en C. D'après la propriété de
Pythagore:
OA2 = AC2 + OC2 . Soit:
(AD - OD)2 = AC2 + OC2
On développe:
AD2 - 2 AD x OD + OD2 = AC2 + OC2
Or OD = OC, donc:
AD2 - 2 AD x OD = AC2 . D'où:
2 AD x OD = AD2 - AC2
OD = (AD2 - AC2)/2 AD =
(802 - 402)/2 x 80 =
(4 x 402 - 402)/4 x 40 =
3 x 402/4 x 40 =
3 x 40/4 = 30
OD = 30 cm
D'où: OA = AD - OD = 80 - 30 = 50 cm.
OA = 50 cm.
Des rapports de Thalès:
OC/OB = OD/OA = DC/AB
, on tire:
DC/AB = OD/OA . Soit:
DC = AB x OD/OA = 40√5 x 30/50 = 24√5
DC = 24√5 = 53.66 cm
•
Le segment [D,C] mesure 53.66 cm.
Exercice 2 : Généralisation du
résultat
de l'exercice 1
Un triangle d'or est un triangle rectangle dont une cathète
est le double de l'autre.
Ecrivons , pour simplifier, AD = BC = 2a , et
BD = AC = a.
Donc
AB = a √5
OD = (3/4) a
DC = (3/5) a √5.
D'où:
OD/OA = OC/OB = DC/AB = 3/5
Théorème
Deux triangles d'or croisés de base commune forment
un trapèze isocèle dont les bases et les
diagonales sont dans le rapport 3/5.
Ce théorème n'existe nul part le 12 avril 2015.
Il est à mon crédit.
|
|