Math�matiques 45: Triangles semblables
Les figures g�om�triques sont congruentes ou isom�triques
si elles ont la m�me taille et la m�me forme. Dans cette section,
nous �tudierons les figures g�om�triques qui ont la m�me forme,
mais pas n�cessairement de la m�me taille. Ces figures
g�om�triques sont appel�s figures semblables ou
similaires.
L'utilisation des triangles semblables a
rendu possible les mesures des hauteurs et
des distances inaccessibles.
1. Figures semblables
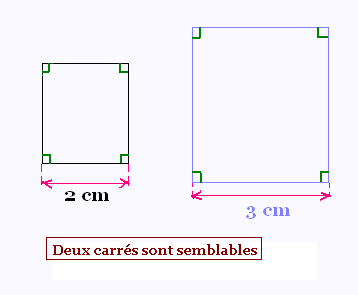
Deux figures sont semblables si l'une est un agrandissement,
une r�duction ou la reproduction exacte de l'autre.
Dans deux figures semblables, les angles
homologues
sont isom�triques et les mesures des c�t�s homologues sont
proportionnelles.
Le rapport de similitude est �gal au rapport de la mesure d'un c�t� de la figure image et de la mesure d'un c�t� de la figure initiale
Rapport de similitude = (mesure d'un c�t� de la figure image)/(mesure d'un c�t� de la figure initiale)
2. Triangles semblables
Deux triangles sont semblables si:
(i) leurs angles homologues sont isom�triques (ou)
(ii) leurs c�t�s homologues sont proportionnels.
Ainsi, deux triangles ΔABC et ΔA'B'C'
sont semblables (similaires) si:
(i) ∠A = ∠A' ∠B = ∠B' ∠C = ∠C' (ou)
(ii) A'B'/AB = B'C'/BC = C'A'/CA
Les sommets A, B et C correspondent aux sommets
A', B' et C' respectivement.
Symboliquement, nous �crivons la similitude
de ces deux triangles comme ΔABC ∼ ΔDEF
et on lit: ΔABC est semblable au ΔA'B'C'.
Le symbole ∼ signifie semblable �.
3. Crit�res de similitude des triangles
Il y a trois crit�res qui sont suffisants pour
prouver que deux triangles sont semblables:
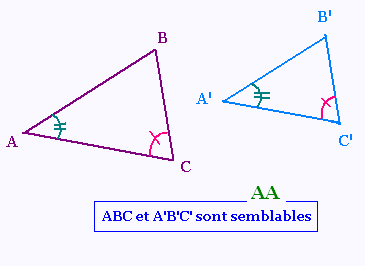
(i) Crit�re de similitude AA (Angle-Angle):
Si deux angles d'un triangle sont respectivement
�gaux � deux angles de l'autre triangle,
alors ces deux triangles sont semblables.
Remarque:
Si deux angles d'un triangle sont
respectivement �gaux � deux angles d'un
autre triangle leurs troisi�mes angles
seront aussi �gaux. Ainsi, le crit�re de similarit�
AA est aussi appel� crit�res AAA.
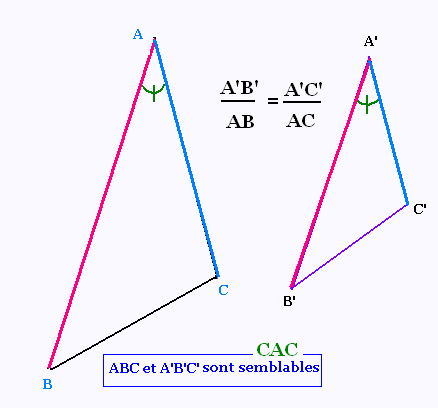
(ii) Crit�re de similarit� CAC(C�t�-Angle-C�t�):
Si une angle d'un triangle est isom�trique � un angle
d'un autre triangle et si les c�t�s correspondants
de ces angles sont proportionnels, alors les deux
triangles sont semblables.
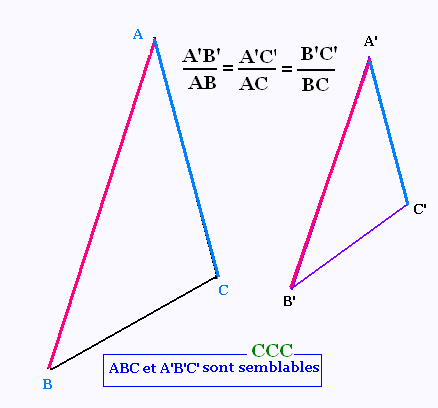
(iii) Crit�re de similarit� CCC (C�t�-C�t�-C�t�):
Si les c�t�s d'un triangle sont proportionnelles
(dans le m�me rapport) aux c�t�s de l'autre triangle,
donc leurs angles homolgues sont isom�triques;
ainsi les deux triangles sont semblables.
|