Mathématiques 45: Géométrie:
Le logiciel Tracenpoche
Exemple: Point mobile le long d'une hypoténuse

1. Construction de la figure


Le couple (x, y) signifie ligne x et colonne y 



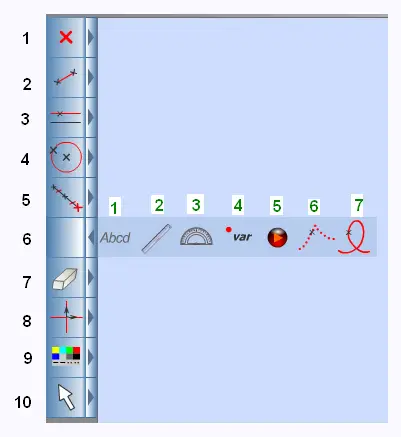Ouvrir Tracenpoche 

Effacer le point A avec (7,1) 
Avec (1,1) placer un point  nommer le R 
Avec (7,5) bouger le nom du pont R
Avec (2,6) placer le S tel que RS = 5 cm 
Avec (3,2) dresser la perpendiculaire au point R 
Avec (4,3) construire un cercle de centre R et de 10 cm
Avec (1,3) marquer le point d'intersection T 
Avec (7,6) Cacher le cercle 
Avec (2,1) tracer le segment ST 
Avec (1,2) construire le point E 
Avec (3,2) dresser la perpendiculaire au segment RT issue du point E 
Avec (1,3) nommer le point d'intersection F
Avec (3,2) dresser la perpendiculaire au segment RS issue du point E 
Avec (1,3) nommer le point d'intersection D 
Avec (2,1) Tracer la diagonale FD  
Avec (6,2) mesurer les diatances FD SE RD et RF

2. Variation de la position du point E
sur l'hypoténuse

Glisser le point E sur ST pour voir 
les mesures changantes de ses segments 

Pour differentes valeurs de SE nous avons differentes 
valeurs de la diagonale DF 

SE varie de 0 au point S a 10.3 au point T 

La diagonale varie de 5 a 10 . Elle passe par un 
minimum qui vaut 4.37.




La variation de FD par rapport a SE n'est pas 
proportionnelle.

3. Position du Point mobile pour un carre


À une certaine position SE,  on obtient un carré:

4. Distance minimale du sommet à l'hypoténuse

Le quadrilatere RFED a trois angles droits; c'est donc  un rectangle. 

Les diagonales d'un rectangles sont isometriques. FD = RE.

Avec (2,1) joindre les points R et E 
Avec (6,3) cliquer sur R, E et S pour mesurer l'angle RES. 


Conjecture: 

Puisque RE est la distance du point R au segment 
ST, la distance FD ou RE est minimale lorsque 
RE est perpendiculaire au segment ST. 





En effet , en glissant le point E sur ST, à la position, on a: 
SE = 2.43 
Fd = 4.37 et 
Mesure (RES) = 90^o. 
 

La distance du sommet de l'angle droit d'un triangle rectangle 
est minimale lorsqu'elle est perpendiculaire à l'hypoténuse.

5. Code de construction de la figure géométrique


@options;
  repereortho(313,263,30,1,1){ 0 , moyen , noir , num1 ,i};

@figure;
  S = point( -4.93 , -2.67 )  { (-0.43,0.63) };
  slongS = segmentlong( S , R , 5 )  { rougefonce , (-1.23,-0.93) };
  perpRslongS = perpendiculaire( R , slongS )  { i };
  cerayR9 = cerclerayon( R , 9 )  { i };
  cerayR91 = cerclerayon( R , 9 )  { i };
  T = intersection( perpRslongS , cerayR91 , 2 )  { rouge , (0.6,0) };
  sTS = segment( T , S );
  sRT = segment( R , T );
  angleSRT = angle( S , R , T );
  E = pointsur( sTS , 0.62 );
  D = projete( E , slongS )  { (-1.33,-0.27) };
  sDE = segment( D , E );
  F = projete( E , sRT )  { (-0.03,-1.3) };
  sEF = segment( E , F );
  pm_disDE = milieu( D , E )  { i };
  tm_disDE = texte( pm_disDE ,"#DE=#")  { noir , (-0.23,1.2) , dec2 };
  pm_disEF = milieu( E , F )  { i };
  tm_disEF = texte( pm_disEF ,"#EF=#")  { rouge , (-4.17,-0.23) , dec2 };
  sDF = segment( D , F )  { vert };
  sRE = segment( R , E )  { rouge };
  pm_disRE = milieu( R , E )  { i };
  tm_disRE = texte( pm_disRE ,"#RE=#")  { noir , dec2 };
  pm_disRF = milieu( R , F )  { i };
  tm_disRF = texte( pm_disRF ,"#RF=#")  { noir , dec2 };
  angleRET = angle( R , E , T );
  tm_mesRET = texte( E ,"#angle(RET)=#Â°")  { noir , (1.03,0.1) , dec2 };
  texte1 = texte( -5.4 , -5.1 ,"E point mobile sur ST")  { noir , dec2 };