Mathématiques: Trigonométrie et Géométrie
Les coordonnées géographiques

1. Les coordonnées géographiques

Pour repérer un point sur le globe terrestre, on utilise les coordonnées géographiques.

Ces coordonnées sont la latitude et la longitude:

• La latitude est une mesure angulaire.

La latitude de référence sur Terre est l'équateur.

La latitude 0 (équateur) s'étend jusqu'au pôle nord (+ 90°) et pôle sud (- 90°).

La latitude associé à un point sur le globe terrestre correspond à la mesure de l'angle au centre qui intrercepte l'arc d'un méridien entre ce point et l'équateur.

• La longitude est une mesure angulaire.

La longitude de référence sur Terre est le méridien de Greenwich.



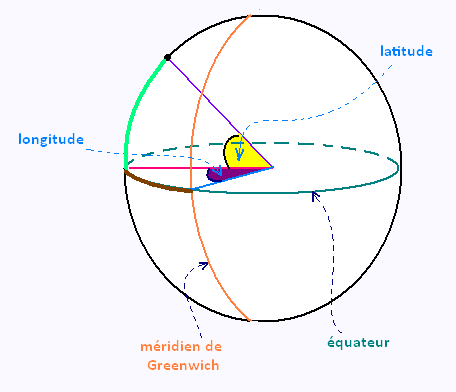
La longitude : 0 (Greenwich) s'étend à l'est jusqu'à + 180^o et à l'ouest jusqu'à - 180^o.

Les coordonnées géographiques sont exprimées dans le système sexagésimal, c'est à dire dans le système à base 60.

La longitude associé à un point sur le globe terrestre correspond à la mesure de l'angle au centre qui intrercepte l'arc de l'équateur entre le méridien de ce point et le méridien de Greenwich.


On utilise les unités suivantes:

le degré d'angle (°), la minute d'angle (') et la seconde d'angle (").

Nous avons les équivalences suivantes:

1 tour complet = 360^o,
la minute d'angle : 1^o = 60',
la seconde d'angle 1' = 60".

On retient:

2. Vitesse d'un point sur un parallèle

Sur Terre, un parallèle est un cercle imaginaire qui relie tous les points situés sur une même latitude.

Un objet fixe sur Terre tourne suivant la rotation de la Terre sur elle même autour de l'axe géographique passant par ses poles. La Terre fait 24 heures pour accomplir un tour complet.

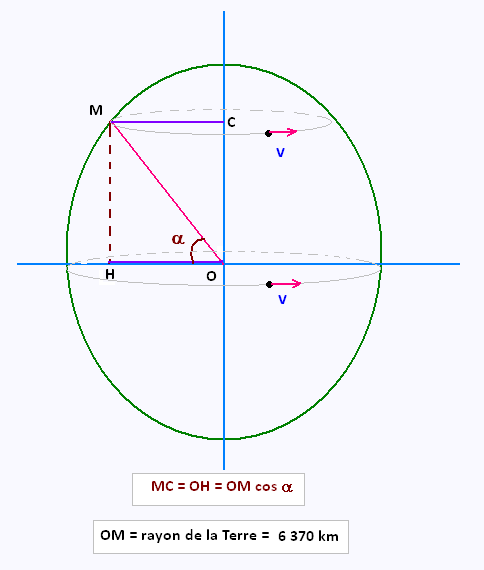
Si un point M sur la Terre a pour latitude α, alors le centre passant par le point M est le parallèle d'angle α.

Nous allons estimer les vitesses auquelles des personnes sont entrainées par la rotation de la Terre lorsqu'elles se trouvent sur différents points du globe:.

Nous avons:

OH = MC et MC/OM = cos α . D'où:

OH = MC = OM cos α

La circonférence C de ce parallèle est égale à 2 π x MC = 2 π x OM cos α

C = 2 π x OM cos α

La vitesse d'un point sur ce cercle est v = C/24 heures

v = 2 π x OM cos α /24 heures = 2 π x 6370 cos α/24 (km/h) =
1667.92 x cos α (km/h)

v = 1667.92 x cos α       (km/h)


Sur l'équateur α = 0. Donc

v = 1667.92 x cos 0 = 1667.92 km/h,
Cette valeur est estimée à 1670 km/h.


a) 45^o 30' = 45^o + 30' = 45^o + 30 x 1^o/60 =
45^o + 30/60 ^o = 45^o + 0.5 ^o = 45.5^o.

45^o 30' = 45.5^o

v = 1670 x cos 45.5 = 1170 km/h

v = 1170 km/h


b) 46^o 49' = 46^o + 30' = 46^o + 49/60 ^o =
46^o + 0.81667 ^o = 46.8167^o.

46^o 49' = 46.8167^o

v = 1670 x cos 46.8167 = 1142 km/h

v = 1142 km/h


c) 50^o 13' = 50^o + 13' = 50^o + 13/60 ^o = 50^o + 0.2167^o = 50.2167 ^o.

50^o 13' = 50.2167 ^o

v = 1670 x cos 50.2167 = 1069 km/h

v = 1069 km/h


d) 58^o 10' = 58^o + 10' = 58^o + 10/60 ^o = 58^o + 0.1667^o = 58.1667 ^o.

58^o 10' = 58.1667 ^o

v = 1670 x cos 58.1667 = 881 km/h

v = 881 km/h

On remarque que plus on monte vers le nord, plus la vitesse devient faible.