Mathématiques
Trigonometrie
Rapports
trigonométriques
Exercices
Calculateur
© The scientific sentence. 2010
|
Mathématiques: Trigonométrie et Géométrie
Géométre des fonctions trigonométriques
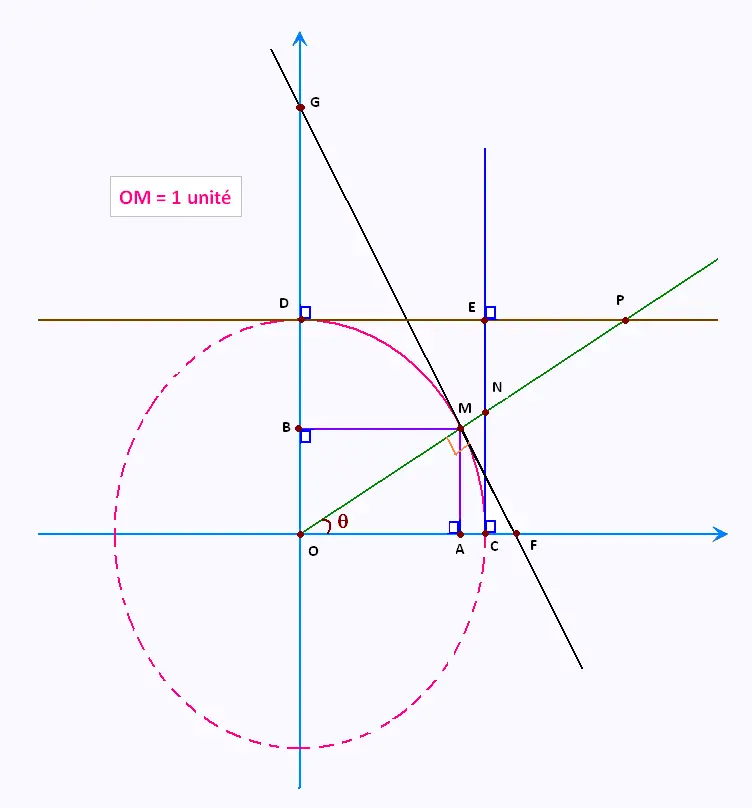
On rappelle que:
• sec(θ) = 1/cos(θ),
• cosec(θ) = 1/sin(θ), et
• cot(θ) = 1/tan(θ)
OM = 1 unité de longeur = OC = OD
OA = BM = cos θ
OA = cos θ
OB = AM = sin θ
OB = sin θ
Les triangles OAM et OCN sont semblables.
D'après le théorème de Thalès OA/OC = AM/CN.
cos θ/1 = sin θ/CN. D'où:
CN = sin θ/cos θ = tan θ.
CN = tan θ
Les triangles OBM et ODP sont semblables.
D'après le théorème de Thalès OB/OD = BM/DP.
sin θ/1 = cos θ/DP. D'où:
DP = cos θ/sin θ = cot θ.
DP = cot θ
La droite (MF) est tangente au cercle en M, elle
est donc perpendiculaire au rayon du cercle OM.
Ainsi, le triangle OMF est rectangle en M.
Ecrivons la relation métrique suivante:
MA2 = AO x AF
AF = OF - OA = OF - cos θ. Donc
sin2 θ = cos θ (OF - cos θ) =
OF x cos θ - cos2 θ
sin2 θ + cos2 θ =
OF x cos θ
1 = cos θ x OF
OF = 1/ cos θ = sec θ
OF = sec θ
Le triangle OMG est rectangle en M.
Ecrivons la relation métrique suivante:
MB2 = BO x BG
BG = OG - OG = OG - sin θ. Donc
cos2 θ = sin θ (OG - sin θ) =
OG x sin θ - sin2 θ
cos2 θ + sin2 θ =
OG x sin θ
1 = OG x sin θ
OG = 1/ sin θ = cosec θ
OG = cosec θ
|
|