Mathématiques 34
Trigonométrie
Loi des cosinus et loi des sinus

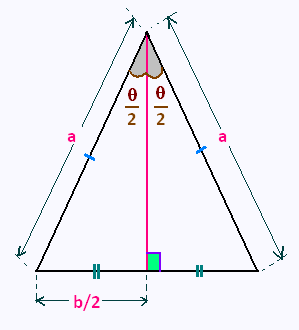
Exercice 1: Triangle isocèle

Rappel:

Dans un triangle isocèle, le segment joignant le sommet principal au milieu du côté opposé est à la fois médiane, hauteur, médiatrice, et bissectrice.


Déterminer le rapport a/b:

a) Par les rapports trigonométriques
b) Par la loi des sinus
c) Par la loi des cosinus


a) sin (θ/2) = (b/2)/a . D'où b/a = 2 sin (θ/2)

b/a = 2 sin (θ/2)

b) (b/2)/sin (θ/2) = a/sin90^o = a. D'où: b/a = 2 sin (θ/2)

b/a = 2 sin (θ/2)

c) b² = a² + a² - 2 a a cos θ = 2 a² - 2 a² cos θ = 2a²(1 - 1 cos θ) . D'où:

b² / a² = 2(1 - cos θ)
(b/a)² = 2(1 - cos θ). Donc:
(b/a) = √[2(1 - cos θ)]

(b/a) = √[2(1 - cos θ)]


Application: θ = 80^o

a) b/a = 2 sin (θ/2) = 2 x sin 40 = 2 x 0.6428 = 1.28557

b) b/a = 2 sin (θ/2) = 1.28557

c) (b/a) = √[2(1 - cos θ)] = √[2(1 - cos 80)] = √[2(1 - 0.17365)] = 1.28557.

Exercice 2: Trois forces

2.1. Longueur de la corde

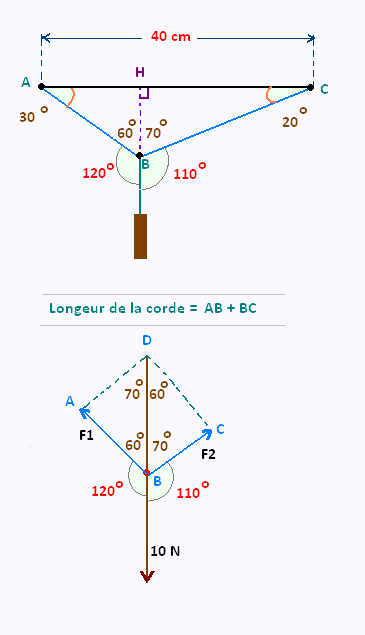
Dreser la perpendiculaire issue de B au segment [AC]. Le point H est le pied de la perpendiculaire.

La droite (AC) est horizontale. La droite (BH) est le support du poids de l'objet suspendu, c'est à dire la verticale.

L'horizontale et la verticale forment un angle droit.

Ainsi, l'angle HBC mesure 70^o et l'angle HBA mesure 60^o. Par conséquent, l'angle HCB mesure 20^o et l'angle HAB mesure 30^o.

Dans le triangle ABC, l'angle saillant B mesure 60^o + 70^o = 130^o. La loi des sinus permet d'ecrire:

AB/sin 20^o = BC/sin 30^o = 40/sin 130^o

Il vient:

AB = 40 sin 20^o/sin 130^o
BC = 40 sin 30^o/sin 130^o

AB = 40 sin 20^o/sin 130^o
BC = 40 sin 30^o/sin 130^o

La longueur de la corde es égale à AB + BC:

AB + BC = 40 sin 20^o/sin 130^o + 40 sin 30^o/sin 130^o =
(40/sin 130^o) (sin 20^o + sin 30^o)
= (40/sin 130^o) (sin 20^o + sin 30^o) = 43.9672 ≈ 44 cm

La corde mesure 44 cm.

2.2. Grandeur des forces du système

ABCD est un parallélogramme de diagonale BD, donc les droites (AB) et (DC) sont parallèles. Ainsi la sécante (BD) forme les angles CDB et ABD alternes internes isométriques et valent chacun 60^o.

De même les angles DBC et BDA sont isométriques et valent chacun 70^o.

Les angles A et C sont isométriques et mesurent chacun 180 - (60 + 70) = 50^o.

BD = 10 N
F1 = AB = DC
F2 = BC = AD

La loi des sinus permet d'ecrire:

10/sin 50 = F2/sin 60 = F1/sin 70 . D'où:

F1/sin 70 = 10/sin 50
F2/sin 60 = 10/sin 50

F1 = 10 sin 70 /sin 50 = 12.267 N
F2 = 10 sin 60 /sin 50 = 11.305 N

F1 = 12.3 N
F2 = 11.3 N

Exercice 3: Le pont Érasme à Rotterdam

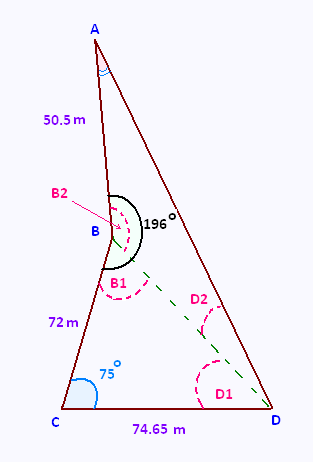
• Dans le triangle CBD, la loi des cosinus s'ecrit:

BD² = BC² + CD² - 2 BC. CD cos C.

BD² = 72² + (74.65)² - 2 (72)(74.65) cos 75 = 7974.4213

BD = 89.2996 ≈ 89.30 m

BD = 89.30 m

• Dans le triangle CBD, la loi des sinus s'ecrit:

CD/sin B1 = BD/sin C

74.65/sin B1 = 89.30/sin 75. D'où:

sin B1 = 74.65 x sin 75 / 89.30 = 0.8075

B1 = sin^-1(0.803) = 53.8485^o

mes (B1) = 53.85^o

• Dans le triangle CBD: mes(D1) = 180 - (75 + 53.85) = 51.15 ^o

mes(D1) = 51.15 ^o

mes(B2) = 196 - mes(B1) = 196 - 53.85 = 142.15^o

mes(B2) = 142.15^o

• Dans le triangle ABD, la loi des cosinus s'ecrit:

AD² = AB² + BC² - 2 AB . BD cos B2 =

50.5² + 89.30² - 2 x 50.5 x 89.30 cos 142.15 = 17646.56

AD = 132.84

AD = 132.84 m

• Dans le triangle ABD, la loi des sinus s'ecrit:

AD/sin B2 = BD/sin A . D'où:

sin B2/AD = sin A/BD

sin A = BD/AD x sin B2 = (89.30/132.84) x sin 142.15 = 0.41248

A = sin^-1(0.41248 ) = 24.36 ^o

mes A ≈ 24.4 ^o

Exercice 4: Mesures dans un triangle quelconque

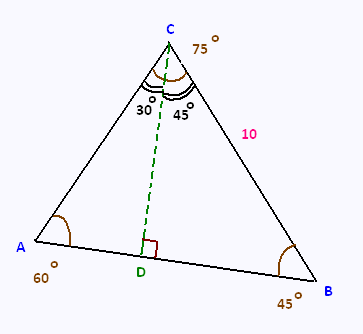
a) • Dans le triangle ABC, la loi des sinus s'ecrit:

AC/sin 45 = 10/sin 60 = AB/sin 75

sin 45 = √2/2
sin 60 = √/2

D'où:

AC = 10 x sin 45/sin 60 = 10 x (√2/2 ) / (√3/2 ) =
10 x (√2 /2) x (2/√3) = 10 x √2/ √3 =
10 x √2 x √3/ 3 = 10 x √6/ 3

AC = 10 √6/3


b) mes (∠BCD) = 90 - 45 = 45^o
mes (∠DCA) = 75 - 45 = 30^o

• Dans le triangle ADC, la loi des sinus s'ecrit:
AC/sin 90 = AD/sin 30

AC = AD/(1/2) = 2 AD    ou    AD = AC/2

• Dans le triangle CDB, la loi des sinus s'ecrit:

10/sin 90 = CD/sin 45
10 = CD/(√2 /2) = 2 CD /√2 = CD √2. D'où:

CD = 10/√2 = 5 √2

CD = 5 √2

• Dans le triangle ADC, la loi des sinus s'ecrit:

AD/sin 30 = CD/sin 60
AD/(1/2) = 5 √2/(√3/2)
2 AD = 10 √2/(√3) = 10 √6 / 3
AD = 5 √6 / 3

AD = 5 √6/3

AC = 2 AD = 10 √6/3

• Dans le triangle CDB, la loi des sinus s'ecrit:

CD/sin 45 = DB/sin 45
CD = DB

BD = CD = 5 √2

AB = AD + DB = 5 √6 / 3 + 5 √2 =
(5 √6 + 15 √2 )/3

AB = (5 √6 + 15 √2 )/3


c) • Dans le triangle ABC, la loi des sinus s'ecrit:

AB/ sin 75 = AC /sin 45 . D'où:

sin 75 = AB x sin 45 / AC = (5 √6 + 15 √2 )/3 x sin 45 / (10 √6 / 3) =
(5 √6 + 15 √2)/3 x (√2 /2)/ (10 √6 / 3) =
(√6 + 3 √2) x (√2 /2)/ (2 √6)
(√12 + 6 ) /4 √6 = (√2 + √6) / 4

sin 75 = (√2 + √6)/4


d) Vérification:

sin 75 = 0.9659
(√2 + √6)/4 = (1.4142 + 2.4495)/4 = 0.9659

Résultats en accord .

Exercice 5: Mesures des côtés dans un polygone

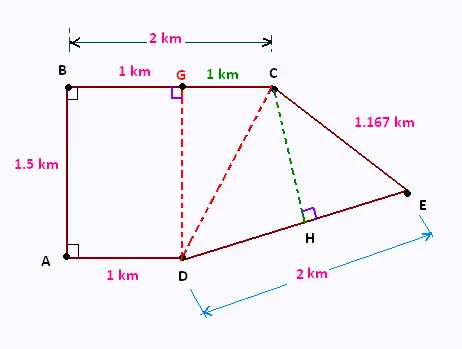
L'angle G est droit. Le théorème de Pythagore s'ecrit:

CD² = 1² + 1.5² = 3.25

CD = 1.80 km .

CD = 1.80 km

• Dans le triangle CDE, la loi des cosinus s'ecrit:

CD² = DE² + CE² - 2 x DE x CE x cos E . D'où:

2 x DE x CE x cos E = DE² + CE² - CD²

cos E = (DE² + CE² - CD²)/(2 x DE x CE) =
(2² + 1.167² - 1.80²)/( 2 x 2 x 1.167) = 0.454561.

cos E = 0.454561

∠E = cos^-1(0.454561) = 62.9633

mes(E) = 63^o

mes(∠E) = 63^o

L'angle H est droit. Donc:

CH/CE = sin E . D'où:

CH = CE x sin E = 1.167 x sin 63 = 1.03946

CH = 1.04 km

CH = 1.04 km

• L'aire du triangle DEC = A1 = DE x CH /2 = 2 x 1.04/2 = 1.04

A1 = 1.04 km²

• L'aire du trapèze rectangle ADCB = A2 = (BC + AD) x AB /2 = (2 + 1) x 1.5 /2 = 2.25

A2 = 2.25 km²

• L'aire du polygone ABCED = A = A1 + A2 = 1.04 + 2.25 = 3.29

L'aire du polygone ABCED = 3.29 km²

Remarque

L'aire du triangle DEC peut être calculée par la formule de Héron:

• Demi-périmètre s = (DE + EC + CD)/2 = (2 + 1.167 + 1.80)/2 = 2.4835

s = 2.4835

• L'aire du triangle DEC est donnée par la formule de Héron:

A1 = √[s(s - DE)(s - EC)(s - CD)]

A1 = √[2.4835 (2.4835 - 2)(2.4835- 1.167)(2.4835 - 1.80)] =
√(2.4835 x 0.4835 x 1.316 x 0.6835) = √1.080 = 1.039

A1 = 1.04 km²

Exercice 6: L'image virtuelle d'un poisson dans l'eau

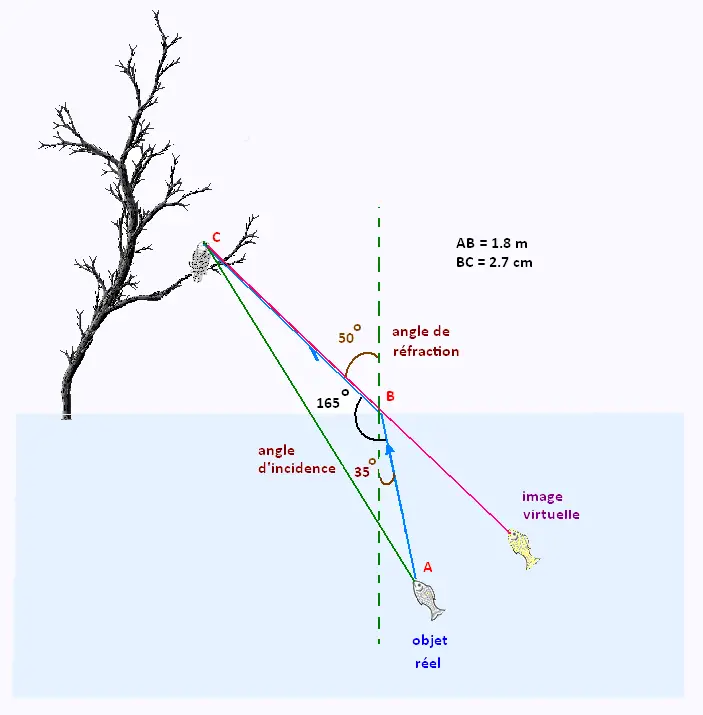
• Dans le triangle ABC, la loi des cosinus s'ecrit:

AC² = AB² + BC² - 2 AB x BC x cos B
= 1.8² + 2.7² - 2 x 1.8 x 2.7 x cos 165 = 19.918799

AC = 4.463 m

AC = 4.463 m

• Dans le triangle ABC, la loi des sinus s'ecrit:

AB/sin C = AC/sin B . D'où:

sin C = AB sin B / AC = 1.8 x sin 165 / 4.463 = 0.104385

C = sin^-1 (0.104385) = 5.992

mes (∠ C) = 6^o

L'aigle voit l'image virtuelle du poisson. Il doit plonger 6^o vers le bas pour tomber réellement sur le poisson.