Mathématiques: Trigonométrie
Loi des sinus
Théorème d'Al-Kachi
Exercices divers: L'ombre sur un mirroir tournant

L'ombre sur un mirroir tournant

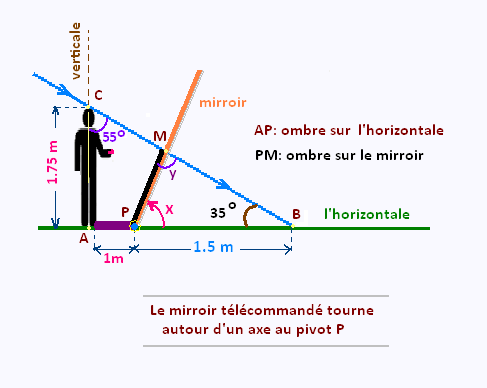
On se propose d'étudier l'ombre d'un objet formée sur un mirroir, d'une certaine inclinaison, tournant utour d'un poivot.

Nous montrerons que cette ombre formée sur le mirroir tournant possède une valeure minimale.

L'angle A est droit.

• Dans le triangle ABC, la loi des sinus s'ecrit:

1.75/sin 35 = AB/sin 55

AB = sin 55 x 1.75/sin 35 = 2.49925

AB = 2.5 m

AB = AP + PB = 1 m + PB. D'où:

PB = AB - AP = 2.5 - 1 = 1.5 m

PB = 1.5 m

Le miroir tourne aoutour du pivot au point P.

Chaque rotation du mirroir correspond à un angle x.

Pour chaque angle $\widehat{x}$, nous avons une ombre PM sur le mirroir.

L'ombre totale est AP + PM.


a) Pour mes $\widehat{x}$ = 65^o, on aura:

mes $\widehat{y}$ = 180 - 65 - 35 = 80^o.

• Dans le triangle BMP, la loi des sinus s'ecrit:

PM/sin 35 = 1.5/sin 80. D'où:

PM = 1.5 x sin 35/sin 80 = 0.8736

PM = 0.87 m. Donc

L'ombre totale = AP + PM = 1 + 0.87 = 1.87 m.

L'ombre totale = 1.87 m


b) Si le mirroir était placé à la verticale, alors x est droit ou mes $\widehat{x}$ = 90^o.

mes $\widehat{y}$= 180 - 90 - 35 = 55^o.

mes $\widehat{y}$ = 55^o.

• Dans le triangle BMP, la loi des sinus s'ecrit:

PM/sin 35 = 1.5/sin 55. D'où:

PM = 1.5 x sin 35/sin 55 = 1.0503

PM = 1.05 m. Donc

L'ombre totale = AP + PM = 1 + 1.05 = 2.05 m.

L'ombre totale = 2.05 m


c) On considère la droite (CB). Le segment [PM] est minimal lorsque la droite (PM) est perpendiculaire à la droite (CB).

C'est à dire que le segment [PM] est la distance du point P à la droite (CB).

Ainsi [PM] est minimal si l'angle $\widehat{y}$ est droit.

Dans ces conditions, l'angle d'inclinaison x du mirroir vaut 90 - 35 = 55^o, c'est à dire les rayons du soleil frappent perpendiculairement le mirroir.

• Dans ce triangle BPM rectangle en B, la loi des sinus s'ecrit:

PM/sin 35 = 1.5/sin 90. D'où:

PM = 1.5 x sin 35/sin 90 = 0.8604

PM = 0.86 m. Donc

L'ombre totale = AP + PM = 1 + 0.86 = 1.86 m.

L'ombre totale minimale = 1.86 m

Une ombre totale plus petite que 1.86 m ne peut pas exister.

En particulier une valeur comme 1.75 m < 1.86 m


Une autre preuve est d'ecrire la loi des sinus dans le «triangle» BMP:

Si l'ombre totale mesure 1.75 alors PM = 0.75, donc

0.75/sin 35 = 1.5/ sin$\widehat{y}$. D'òu;

sin $\widehat{y}$ = 1.5 x sin 35 / 0.75 = 1.4715

sin $\widehat{y}$ = 1.5 !! . Un sinus plus grand que 1 !!

Il n'est pas possible de déterminer un tel angle $\widehat{y}$ qui formerait ce triangle (BMP).

Il n'est donc ainsi pas possible d'avoir une inclinaison du mirroir pour que l'ombre formée sur lui soit plus petite que 1.86 mètres.