Mathématiques
Trigonometrie
Rapports
trigonométriques
Exercices
Calculateur
© The scientific sentence. 2010
|
Mathématiques: Trigonométrie
Loi des sinus
Théorème d'Al-Kachi
Exercices divers: Drapeau de Seychelles
Drapeau de Seychelles
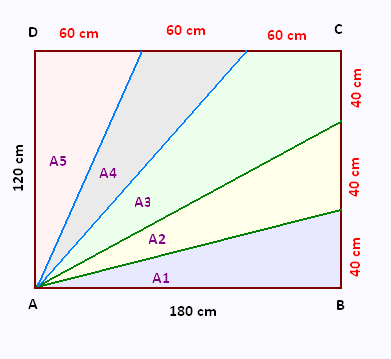
a)
L'angle est droit.
• Mesure de l'angle :
tan () = 40/180
= 0.2222
mes () =
tan-1 (0.2222) = 12.53o
mes () =
12.5o
• Mesure de l'angle :
tan ( +
) = (40 + 40)/180
80/180 = 0.444
mes ( +
) =
tan-1 (0.4444) = 23.96o
mes () = 23.96o
- mes(
) =
23.96 - 12.53 = 11.43o
mes () =
11.4o
L'angle est droit.
• Mesure de l'angle :
tan () = 60/120
= 0.50
mes () =
tan-1 (0.5) = 26.56o
mes () =
26.6o
• Mesure de l'angle :
tan ( +
) = (60 + 60)/180
120/120 = 1
mes ( +
) =
tan-1 (1) = 45o
mes () = 45o
- mes(
) =
45 - 26.56 = 18.43o
mes () =
18.4o
• Mesure de l'angle
= 90o -
mes () -
mes () -
mes () -
mes ()
) =
90o -
12.5 - 11.4 - 18.4 - 26.6
= 21.1o
= 21.1o
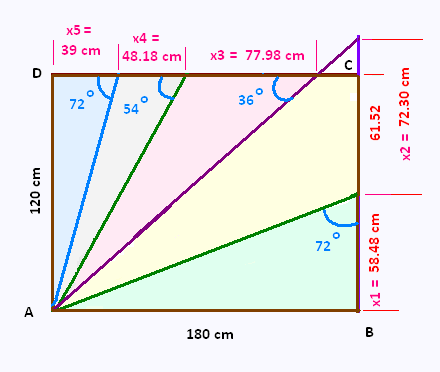
b) Si les angles sont isométriques, alors
90o = 5 x la mesure d'un angle. Ainsi:
La mesure d'un angle est: 90/5 = 18o
Mesure d'un angle est 18o.
Dans ce cas:
tan 18 = x1/180.
D'où :
x1 = 180 x tan 18 = 58.48 cm.
x1 = 58.48 cm
tan(18 + 18) = (x1 + x2)/180. D'où :
x1 + x2 = 180 x tan 36 =
= 130.78.
x2 = 130.78 - x1 = 130.78 - 58.48 = 58.48
x2 = 72.30 cm
130.78 - 120 = 10.78
72.30 - 10.78 = 61.52
61.52
tan 18 = x5/120. D'où :
x5 = 120 x tan 18 = 38.99 cm
x5 = 38.99 = 39 cm
tan(18 + 18) = (x5 + x4)/120. D'où :
x5 + x4 = 120 x tan 36 =
= 87.18 cm .
x4 = 187.18 - x5 = 87.18 - 39 = 48.18
x4 = 48.18 cm
tan(18 + 18 + 18) = (x5 + x4 + x3)/120. D'où :
x5 + x4 + x3 = 120 x tan 54 =
165.16 cm .
x3 = 165.16 - (x5 + x4) = 165.16 - 87.18 = 77.98
x3 = 77.98 cm
La region de l'angle A2 n'est plus un triangle, mais
un quadrilatère comme elle était la région
d'angle A3 en a) .
Remarque
les calculs en b) peuvent bien être fait
au moyen des lois de sinus et cosinus.
|
|