Mathématiques
Trigonometrie
Rapports
trigonométriques
Exercices
Calculateur
© The scientific sentence. 2010
|
Mathématiques: Trigonométrie
Loi des sinus
Théorème d'Al-Kachi
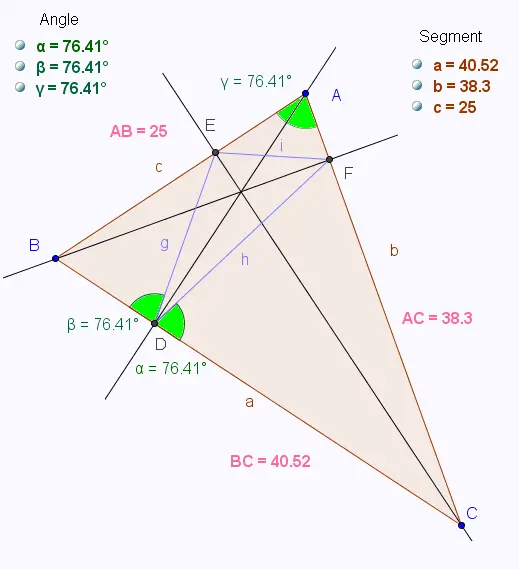
Exercices divers: Angles et hauteurs dans un triangle
Angles et hauteurs dans un triangle
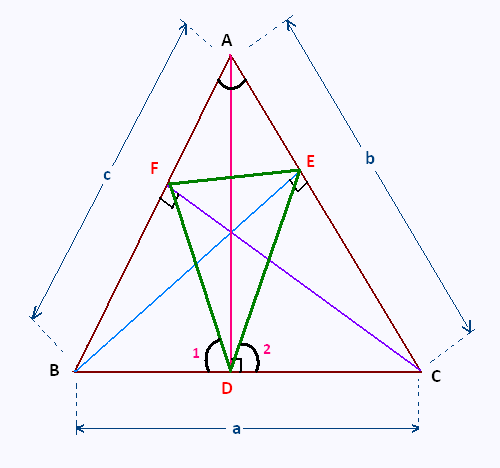
ABC est un triangle quelconque.
Les angles D, E, et F sont droits.
Application:
AB = c = 10 cm
BC = a = 13 cm
AC = b = 15 cm
a)
• Dans le triangle ABC, la loi des cosinus s'ecrit:
a2 = b2 + c2 - 2 bc cos A
b2 = a2 + c2 - 2 ac cos B
c2 = a2 + b2 - 2 ab cos C
cos A = (b2 + c2 - a2)/2bc
cos B = (a2 + c2 - b2)/2ac
cos C = (a2 + b2 - c2)/2ab
cos A = (152 + 102 - 132)/2 x 10 x 15 =
0.52
mes = cos-1 (0.52) = 58.67
mes = 58.67o
cos B = (132 + 102 - 152)/2 x 13 x 10 =
0.169
mes =
cos-1 ( 0.169) = 80.27
mes = 80.27o
cos C = (132 + 152 - 102)/2 x 13 x 15 =
= 0.754
mes =
cos-1 (0.7538) = 41.07
mes =
41.07 o
b)
• Dans le triangle rectangle BFC :
BF/BC = cos
BF = a cos
BF = 13 cos 80.27 = 2.20 m
BF = 2.20 m
• Dans le triangle rectangle BDA :
BD/AB = cos
BD = c cos
BD = 10 cos 80.27 = 1.69
BD = 1.69 m
• Dans le triangle rectangle ADC:
DC/AC = cos
DC = b cos
DC = 15 cos 41.07 = 11.31 m
DC = 11.31 m
• Dans le triangle rectangle BEC:
CE/BC = cos
CE = a cos
CE = 13 cos 41.07 = 9.80
CE = 9.80 m
c)
• Dans le triangle BDF, la loi des cosinus s'ecrit:
FD2 = BF2 + BD2 - 2 . BF . BD cos
FD2 = 2.202 + 1.692 - 2 x 2.20 x 1.69 cos 80.27 = 6.44
FD = 2.54
FD = 2.54 m
• Dans le triangle DEC, la loi des cosinus s'ecrit:
DE2 = DC2 + EC2 - 2 . DC . EC cos
DE2 = 11.312 + 9.802 - 2 x 11.31 x 9.80 cos 41.07 = 56.83
DE = 7.54
DE = 7.54 m
d)
• Dans le triangle BFD, la loi des sinus s'ecrit:
BF/sin = FD/sin
sin =
BF sin / FD
sin = 2.20 sin 80.27 / 2.54
= 0.85368
mes = sin-1
(0.85368 ) = 58.61
mes =
58.610
• Dans le triangle EDC, la loi des sinus s'ecrit:
EC/sin = ED/sin
sin = EC sin / ED
sin = 9.80 sin 41.07 / 7.54
= 0.8539
mes = sin-1
( 0.8539 ) = 58.64
mes =
58.640
Au dixième près, mes =
mes =
mes = 58.70
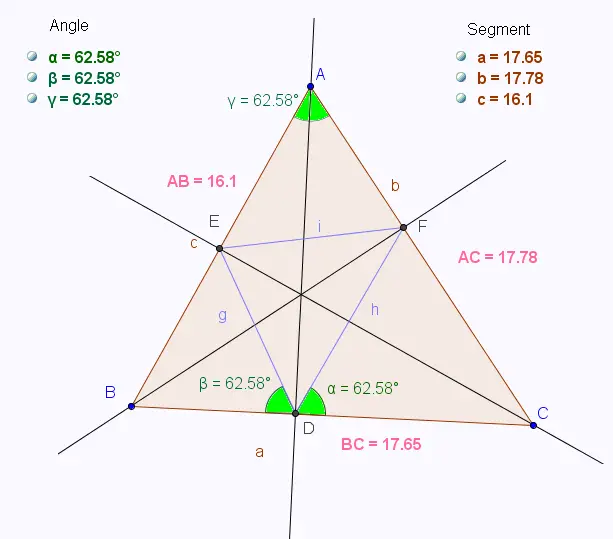
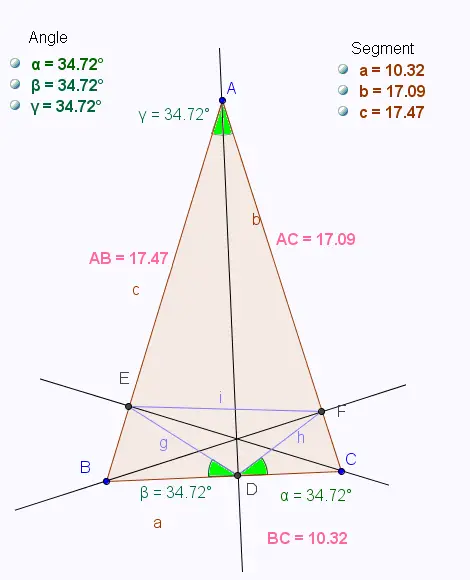
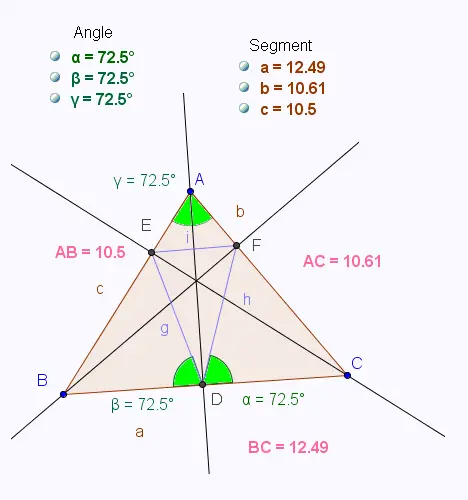
La conjecture pour l'isométrie de ses angles est vraie.
Sur un logiciel de Géométrie, si on change les côtés du triangle,
les angles ,
, et
changent,
mais ils restent toujours isométriques.
• Avec Geogebra
|
|