Mathématiques 2: Trigonométrie

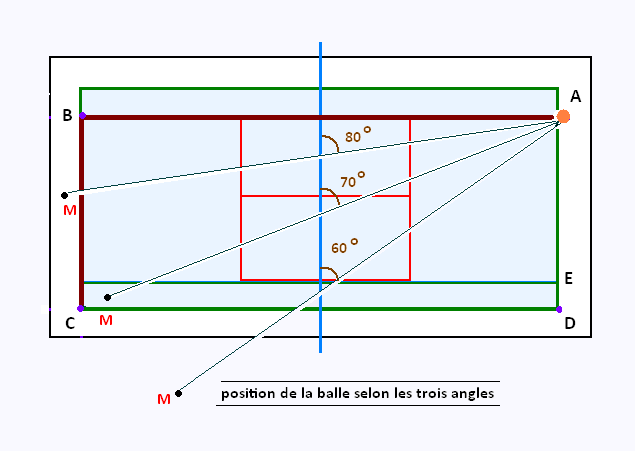
1. Sur le terrain de tennis

Dans une partie de tennis en double, on frappe la balle à partir du point A. La distance de la balle est fixée et est égale à 24.6 m.

La trajectoire de la balle forme un angle variable x avec le filet.



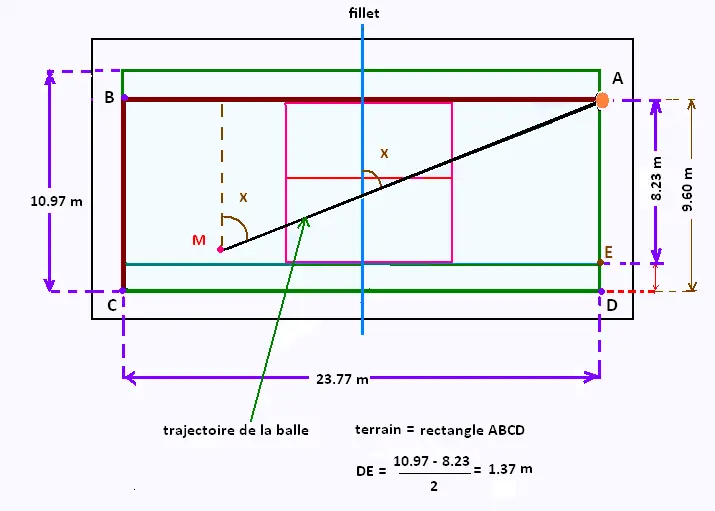
On se propose de déterminer, selon trois valeurs de l'angle x, si la balle tombe à l'intérieur ou à l'exterieur du terrain ABCD.

a)







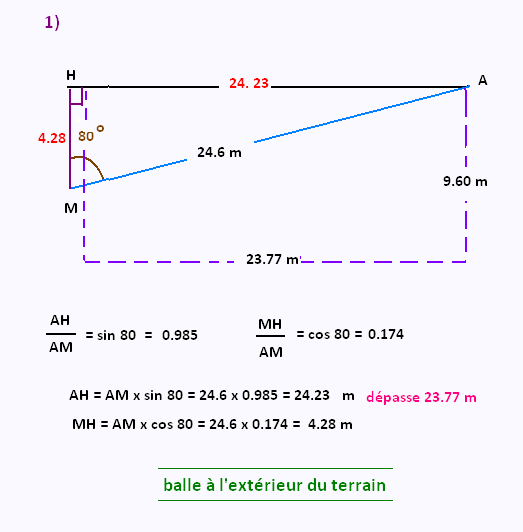
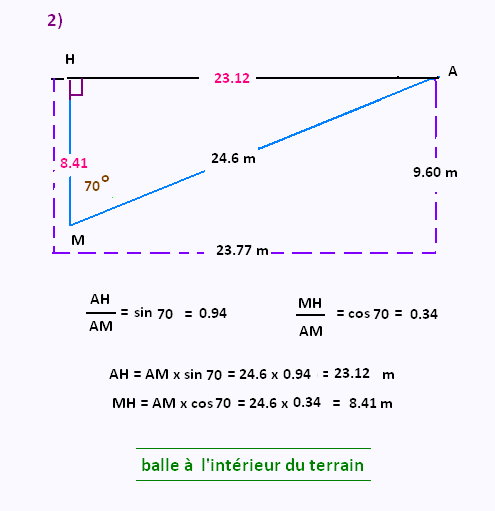
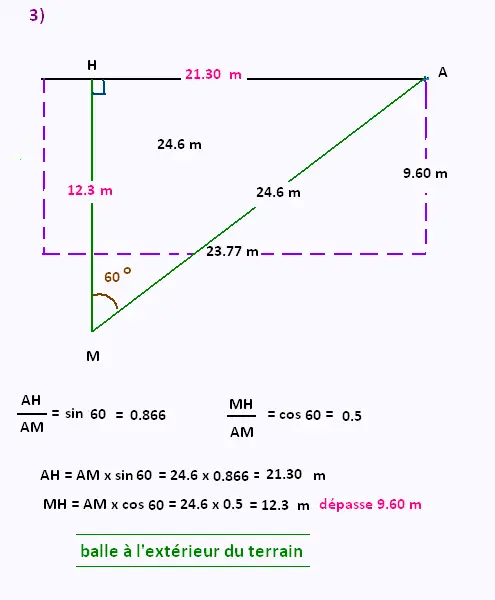
b)

2. Polynomes réguliers

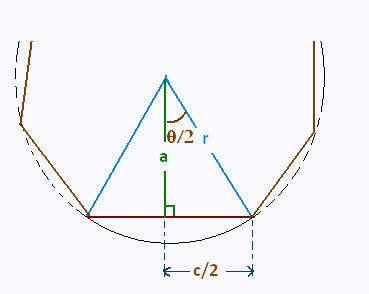
Pour un polygone régulier:

n est le nombre de côtés
a est l'apothème
c est le côté
r est le rayon du cerle circonscrit au polygone.

P = Périmètre du polygone = somme des côtés = n x c

A = Aire du polygone = can/2

Co = Circonférence du cercle = 2 π r
Ao = Aire de disque = π r²

Si le polygone contient n côtés, alors l'angle au centre θ formé par deus rayons r est égal à 360^o/n.

θ = 360^o/n

On a donc : cos(θ/2)= a/r = a/10. D'où :

a = r cos(θ/2) = r cos (180^o/n)

Le triangle formé par le sommet &thta; est isocèle puisque ses deux côtés sont les rayons r d'un même cercle.

D'après la propriété:
Dans un triangle isocèle la hauteur issue du sommet est aussi médiane du côté opposé à ce sommet.

Donc l'apotème partage le côté opposé au sommet en deux. Nous aurons donc:

(c/2) / r = sin (θ/2). D'où:

c = 2 r sin (θ/2) = 2 r sin (180^o/n)

c = 2 r sin (180^o/n)

P = n c = 2 r n sin (180^o/n)
A = can/2 = 2 r sin (180^o/n) x r cos (180^o/n) x n /2
= n r² sin (180^o/n) x cos (180^o/n)

P = 2 r n sin (180^o/n)

A = n r² sin (180^o/n) x cos (180^o/n)


1. Pentagone

P = 2 r n sin (180^o/n) = 2 x 10 x 5 x sin (180/5) = 58.8 cm

% périmètre = n sin (180^o/n)/π = 5 sin (180^o/5) / π = 93.6%.

A = n r² sin (180^o/n) x cos (180^o/n) =
5 x (10)² sin (180^o/5) x cos (180^o/5)
= 273.76 cm².

% aire = n sin(180^o/n) cos(180^o/n)/π
= 5 sin(180^o/5) cos(180^o/5)/π = 75.7%

2. Pourcentages:

Des périmètres:

Périmètre du polygone/Circonférence du cercle= P/Co =
2 r n sin (180^o/n)/2 π r = n sin (180^o/n)/π

% périmètre = n sin (180^o/n)/π

Des aires:

Aire du polygone/Aire de disque = A/Ao =
n r² sin(180^o/n) x cos(180^o/n) / π r² =
n sin(180^o/n) x cos(180^o/n)/π

% aire = n sin(180^o/n) cos(180^o/n)/π

On dresse un tableau avec r = 10 cm :

figure	décagone régulier	polygone régulier à 20 côtés	polygone régulier à 100 côtés
Mesure de l'apothème (cm)	9.51	9.87	9.99
Mesure des côtés (cm)	6.18	3.13	0.63
Rapport du périmètre de la figure à la circonférence du cercle (%)	98.4	99.6	99.98
Rapport dde l'aire de la figure à l'aire du disque (%)	93.5	98.4	99.93