Maths
- 45 -
Les vecteurs
Partie 1
Partie 2
© The scientific sentence. 2013
|
| Mathématiques 45: Algèbre vectorielle:
Décomposition d'un vecteur
Combinaison linéaire de vecteurs
Base vectorielle
1. Combinaison linéaire de vecteurs
La somme de deux vecteurs donne un vecteur résultant. Réciproquement,
un vecteur est décomposable en deux autres vecteurs.
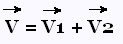
En pratique, sur un plan, on décompose un vecteur
en deux autres vecteurs; et dans l'espace, on décompose un
vecteur en trois autres.
À leur tour, les vecteurs obtenus par décomposition, peuvent
s'ecrire sous forme d'un produit d'un scalaire et d'un vecteur:
 = k1 = k1 et
et
 = k2 = k2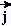
Ainsi
 = k1 = k1 + k2 + k2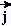
Cette ecriture est appelée combinaison linéaire des vecteurs
 et et 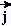 . .
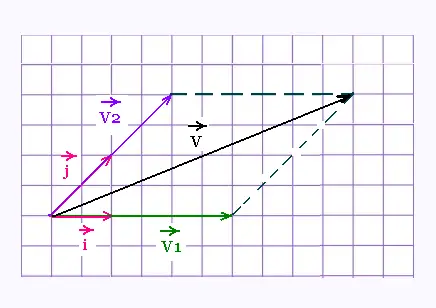
Une combinaison linéaire permet donc de construire un vecteur
résultant en partant des vecteus connus  et et
 . .
Les facteurs k1 et k2 sont appelés les coefficients de la
combinaison.
2. Base vectorielle
Deux vecteurs, à partir desquels, on peut
former un autre vecteur, constituent une base vectorielle.
Ces deux vecteurs doivent évidemment être linéairement indépendants,
c'est à dire non égaux et non parallèles.
La base vectorielle la plus simple est la plus utilsée
et la base orthonormée. Elle est em même temps
normée et orthogonale.
La base { , ,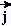 } est
normée si ses vecteurs sont normés; c'est à dire leur norme
égale à 1 : } est
normée si ses vecteurs sont normés; c'est à dire leur norme
égale à 1 :
|| || = || || = ||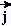 || = 1 || = 1
Elle est orthogonale si ses vecteurs sont orthogonaux; c'est à dire
leur produit scalaire est nul:
 • •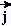 = 0. = 0.
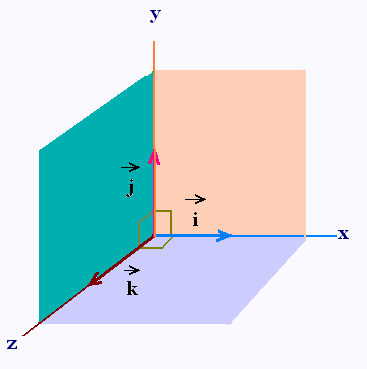
Un système d'axes appelé repère est orthonormé s'il est
muni d'une base orthonormée.
Voici un repère orthonormé à 3 dimensions:
|
|