Maths
- 45 -
Les vecteurs
Partie 1
Partie 2
© The scientific sentence. 2013
|
| Mathématiques 45: Algèbre vectorielle:
Opérations sur les vecteurs
Produit vectoriel
1. Introduction
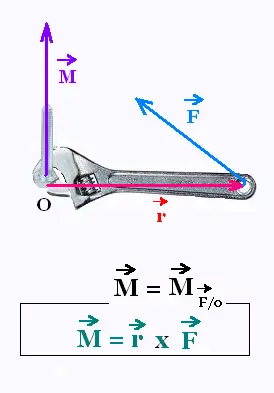
Lorsqu'on veut serrer un écrou ou le débloquer
avec une clé à molette, Il est nécessaire
d'exercer une force sur la clé.
L'effet sur l'ecrou est appréciable lorsque
les trois conditions suivantes sont satisfaites:
• La force exercée sur la clé est grande,
• Le bras de levier est grand,
• L'orientation de la force est perpendiculaire
au bras de levier.
Bras de levier = distance entre l'ecrou est le point
d'application de la force.
L'ensemble des trois conditions citées est
équivalent au terme de moment de la force.
L'effet sur l'ecrou est appréciable lorsque le
moment de la force exercée est apprciable.
Par définition, le moment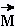 de la
force de la
force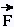 exercée à ue distance r
du centre O est le produit vectoriel de exercée à ue distance r
du centre O est le produit vectoriel de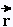 et de
et de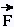 .
On l'ecrit: .
On l'ecrit:
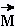 = = 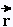 x x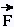
Le symbole x désigne le produit
scalaire. On le note aussi par le symbole . .
Le vecteur est appelé vecteur position. Son
origine est le centre de rotation O. est appelé vecteur position. Son
origine est le centre de rotation O.
Le moment d'une force par rapport à un point fixé est
une grandeur physique qui est vectorielle.
1. Définitions
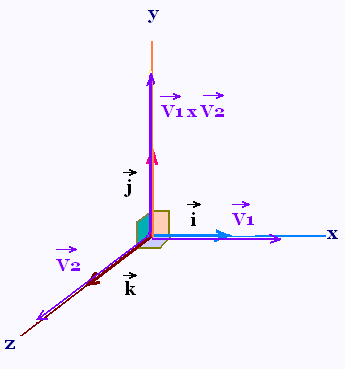
Le produit vectoriel de deux
vecteurs est un vecteur.
Dans le plan cartésien, le produit vectoriel de deux
vecteurs est un vecteur qui est perpendiculaire au
plan formés par les deux vecteurs initiaux.
Ainsi l'opération produit vectoriel nécessite un
système de référence à trois dimensions:
deux dimensions pour le plan qui comprend
les deux premiers vecteurs et une troisième dimension pour
la droite qui doit supporter le vecteur produit
vectoriel résultat.
Le produit vectoriel nécessite des vecteurs avec
trois composantes.
Le produit vectoriel de deux vecteurs et
et est défini par sa norme: est défini par sa norme:
|| x x || =
|| || =
|| || || || || || sin θ || sin θ
θ est l'angle formé par les deux vecteurs
.
Le vecteur  x x est un
vecteur est un
vecteur . Le support de ce produit vectoriel
est une drooite perpendiculaire au plan formé par les vecteurs . Le support de ce produit vectoriel
est une drooite perpendiculaire au plan formé par les vecteurs et
et . .
En termes de composantes des deux vecteurs, si
 (x1, y1, z1) et (x1, y1, z1) et  (x2, y2, z2),
alors les composantes du vecteur (x2, y2, z2),
alors les composantes du vecteur  x x sont:
sont:
(y1z2 - y2z1, x2z1 - x1z2, x1y2 - x2y1)
3. Exemple
Soient les vecteurs suivants:
 (1, 0, 0) et (1, 0, 0) et (0, 1, 0) (0, 1, 0)
Leur produit vectoriel est le vecteur
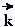 = =  x x 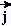
de composantes (0x0 - 1x0, 0x0 - 1x0, 1x1 - 0x0) = (0, 0, 1).
Sa norme est || || || || ||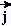 || sin 90° =
1 x 1 x 1 = 1. || sin 90° =
1 x 1 x 1 = 1.
Ainsi le vecteur 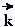 est normé. est normé.
Dans le repère (O, x, y, z),  se trouve sur
l'axe Ox, se trouve sur
l'axe Ox,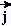 sur l'axe Oy et leur produit vectoriel sur l'axe Oy et leur produit vectoriel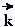 sur l'axe Oz.
sur l'axe Oz.
|
|