Mathématiques 45: Algèbre vectorielle:
Propriétés des opérateurs sur les vecteurs

On vérifie facilement les propriétés suivantes:

1. Addition de deux vecteurs

1. Fermeture:
L’addition de deux vecteurs donne un vecteur.
+ =

2. Commutativité:
L’addition de vecteur est commutative.
+ = +

3. Associativité:
L’addition de vecteurs est associative .
+ ( +) = ( +) +

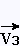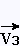
4. L’addition de vecteurs possède un élément
neutre, qui est le vecteur nul.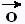

2. Multiplication d’un vecteur par un scalaire

1. Le produit d’un vecteur par un scalaire est un vecteur.
k =

2. Associativité:
Le produit d’un vecteur par des scalaires est associative.
k1(k2) = (k1k2)

3. Le scalaire 1 est l’élément neutre.

1 =

4. Distributivité : Le produit d'une somme de vecteurs par un scalaire est distributive.

k( + ) = k + k

5. Distributivité :
Le produit d'un vecteur par une somme de scalaires est distributive .
(k1 + k2) = k1 + k2

3. Propriétés de la multiplication scalaire
de deux vecteurs.

1. La fermeture n'est pas vérifiée: Le produit de deux vecteurs est un scalaire et non un vecteur.

• = a (scalaire = réel)

2. Commutativité:
La multiplication scalaire de deux vecteurs est cmmutative.
• = •

3. Distributivité sur l’addition de vecteurs:
La multiplication scalaire d'un vecteur par une somme de vecteur est associative.
• ( +) = • + •

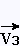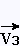
4. Associativité:
La multiplication des produits de scalires et vecteurs est associative.
k1 • k2 = (k1k2) •

5. Associativité:
Le produit scalaire des vecteurs n'est pas associatif.
• ( •) ≠ ( •) •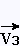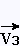