Maths
- 45 -
Les vecteurs
Partie 1
Partie 2
© The scientific sentence. 2013
|
|
Mathématiques 45: Algèbre vectorielle:
Les vecteurs
1. Définition
Une quantité est scalaire si elle est définie par un nombre réel.
Une quantité est vectorielle si elle est définie par un vecteur.
Un vecteur est une quantité défini à la fois par
une grandeur, une direction et un
sens.
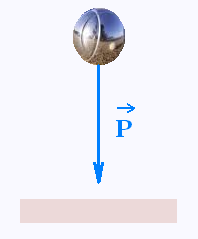
Le poids d'un objet est un vecteur.
Sa grandeur , c'est combien il mesure en unités de
force qui est le Newton.
Sa direction c'est la verticale.
Son sens , c'est "vers le bas".
2. Géométrie d'un vecteur
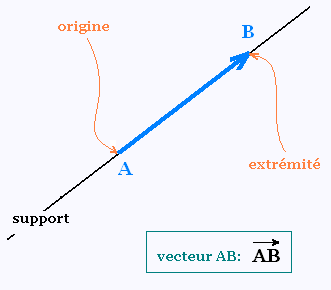
On représente un vecteur par un segment et
une flèche.
L’axe sur lequel se trouve un vecteur
s'appelle le support de ce vecteur.
Un vecteur possède un point de départ appelé origine et un point d'arrivée appelé extrémité. C'est l'extrémité du vecteur qui
contient la flèche.
Le segment AB se nomme vecteur AB. Le vecteur AB a pour origine A, et pour extrémité B.
Il s'ecrit 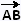 . .
Sur un dessin, la mesure du trait qui représente de la longueur d'un vecteur est appelé sa valeur algébrique.
L'orientation d'un vecteur est l'angle anti-horaire entre le demi-axe Ox et le support du vecteur.
Exemple:
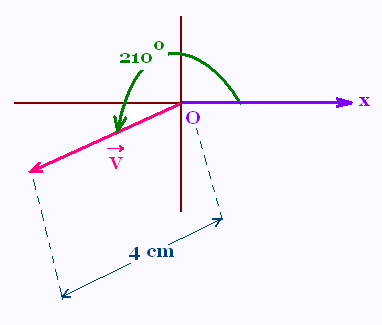
La grandeur du vecteur est de 4 cm. est de 4 cm.
L’orientation est de 210°.
Un vecteur de grandeur 0 s’appelle vecteur nul. On le symbolise par . .
3. Vecteurs dans un plan cartésien
3.1. Composantes et norme d'un vecteur
Les composanes d'un vecteur sont les
variations des abcisses Δx et des ordonnées
Δy en partant de l'origine jusqu'à l’extrémité de la flèche du vecteur.
De l'origine A, à l’extrémité B , le déplacement
est de 7 unités vers la droite et de 5 unités
vers le haut.
• e déplacement vers la droite Δx = xb - xA = 7 unités.
• Le déplacement vers le haut Δy = yb - yA = 5 unités.
Ces deux nombres Δx = 7 et Δy = 5
sont exactement les cmposantes du vecteur AB.
On ecrit:
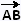 (Δx, Δy). (Δx, Δy).
La norme d'un vecteur est égale à sa grandeur,
c'est à dire la distance entre son extrémité et son origine.
La norme du vecteur AB s'ecrit: ||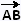 ||. ||.
3.2. Exemple
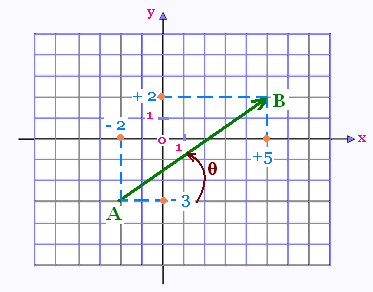
Le vecteur 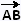 a rour origine A(- 2, - 3) et pour extrémité B(+ 5, + 2). a rour origine A(- 2, - 3) et pour extrémité B(+ 5, + 2).
Sa norme est égale à la distance entre le point A et
le point B. C'est à dire:
||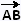 || = d(A, B) = √[(xB - xA)2 + (yB - yA)2] =
√[Δx2 + Δy2] || = d(A, B) = √[(xB - xA)2 + (yB - yA)2] =
√[Δx2 + Δy2]
||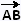 || =
√[72 + 52] =
√[49 + 25] = √74 = 8.60. || =
√[72 + 52] =
√[49 + 25] = √74 = 8.60.
||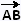 || = 8.60 unités. || = 8.60 unités.
L’orientation du vecteur AB est l'angle anti-horaire θ entre le demi-axe horizontal (ox) et la droite (AB).
On calcul l'angle anti-horaire au moyen de la tangente:
tan θ = Δy/Δx = 5/7 = 0.71
Ainsi θ = tan- 1(0.71) =
35.54°
|
|