Maths
- 45 -
Les vecteurs
Partie 1
Partie 2
© The scientific sentence. 2013
|
|
Mathématiques 45: Vecteurs:
Vecteurs colinéaires
1. Vecteurs colinéaires
Deux vecteurs  et et  non nuls et sont colinéaires s'ils sont proportionneles, c'est à dire s’il existe un nombre réel k tel que : non nuls et sont colinéaires s'ils sont proportionneles, c'est à dire s’il existe un nombre réel k tel que :
 = k = k
Autrement dit, deux vecteurs sont colinéaires si l’un est un multiple de l’autre.
Le vecteur nul est colinéaire à tous les vecteurs.
Dans un repère quelconque, les vecteurs  (x1,y1) et (x1,y1) et  (x2,y2) sont colinéaires si et seulement si : (x2,y2) sont colinéaires si et seulement si :
x1y2 = x2y1
Deux vecteurs colinéaires sont placés sur um même support ou deux supports parallèles.
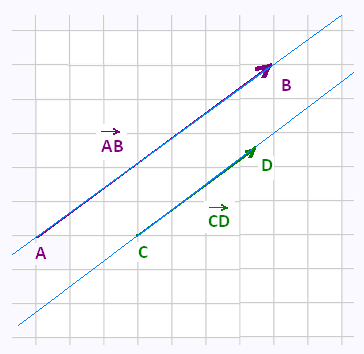
La colinéarité de deux vecteurs permet de démontrer que deux droites sont parallèles. On utilise la propriété suivante :
Les droites (AB) et (CD) sont parallèles si et seulement si les vecteurs 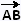 et et 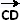 sont colinéaires. sont colinéaires.
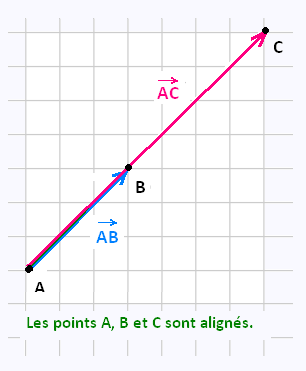
La colinéarité de deux vecteurs permet de démontrer que trois points sont alignés. On utilise la propriété suivante :
Les points A, B, et C sont alignés si et seulement si les vecteurs 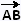 et et 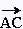 sont colinéaires. sont colinéaires.
2. Somme de deux vecteurs colinéaires
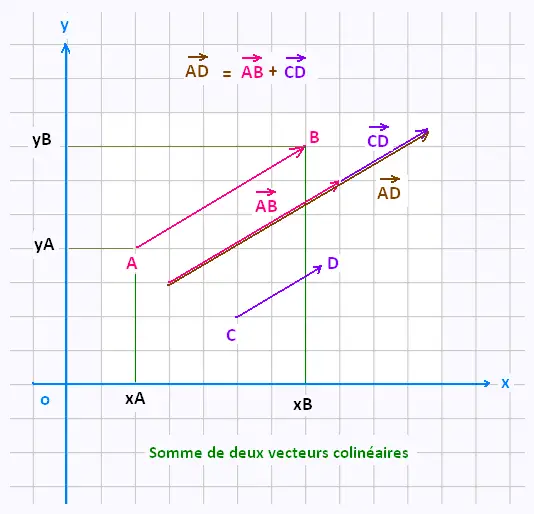
Si deux vecteurs 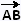 et et 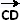 sont colinéaires , la norme de la somme
est égale à la somme des normes deux vecteurs: sont colinéaires , la norme de la somme
est égale à la somme des normes deux vecteurs:
||  + + || = || || = || || + || || + || || ||
|
|