Maths
- 45 -
Les vecteurs
Partie 1
Partie 2
© The scientific sentence. 2013
|
|
Mathématiques 45: Algèbre vectorielle:
Comparaison des vecteurs
1. Comparons des vecteurs

Deux vecteurs sont égaux s’ils ont la même grandeur, la même direction et le même sens.
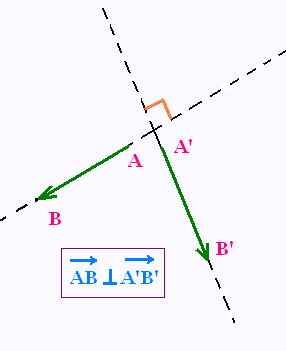
Deux vecteurs sont perpendiculaires ou orthogonaux si leur support forment un
angle droit.
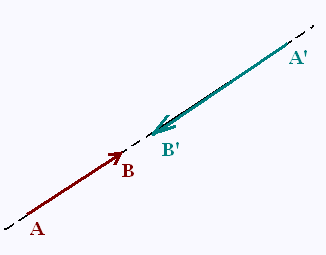
Deux vecteurs sont opposés si leur sens
sont opposés.
Le vecteur opposé du vecteur 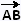 est
le vecteur est
le vecteur 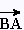 = - = -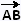 . .
Deux vecteurs opposés 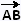 et et
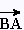 vérifient: vérifient:
||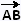 || = || || = ||  || ||
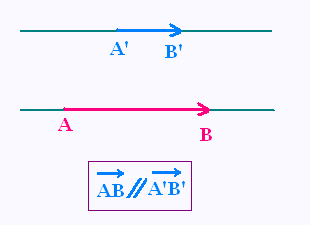 Deux vecteurs sont parallèles si leur supports
sont parallèles.
Deux vecteurs sont parallèles si leur supports
sont parallèles.
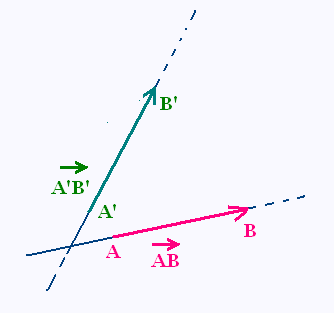
Deux vecteurs sont colinéaires ou linéairement dépendants si leur supports sont parallèles ou confondus.
Deux vecteurs parallèles, deux vecteurs
opposés, ou deux vecteurs égaux sont colinéaires.
 Deux vecteurs sont linéairement indépendants s'ils ne sont pas linéairement dépendants. C'est à dire leurs directions forment un angle autre que l'angle plat.
Deux vecteurs sont linéairement indépendants s'ils ne sont pas linéairement dépendants. C'est à dire leurs directions forment un angle autre que l'angle plat.
2. Exemple
Si les coordonnés d'un vecteur  sont ( - 2, + 3), alors: sont ( - 2, + 3), alors:
• Les coordonnées d'un vecteur parallèle à  sont des multiples de celles du vecteur sont des multiples de celles du vecteur  , par exemple (- 4, + 6) ou ( - 1, + 3/2) ou (+ 8, - 12). , par exemple (- 4, + 6) ou ( - 1, + 3/2) ou (+ 8, - 12).
• Les coordonnées d'un vecteur à opposé à  sont (+2, - 3). sont (+2, - 3).
On peut vérifier que || || = ||- || = ||- || ||
√[(- 2)2 + (+ 3)2] =
√[(+ 2)2 + (- 3)2] = √13.
• Les coordonnées d'un vecteur orthogonal à  sont (+ 3, + 2) ou (- 3, - 2). sont (+ 3, + 2) ou (- 3, - 2).
Ici, il suffit juste d'inverser les coordonnées et changer le
signe de l'une d'entre elles.
Nous verrons que les coordonnées de deux vecteurs orthogonaux, dans un repère orthonormé, (x1, y1) et (x1, y1) et (x2, y2) verifient la relation:
x1 x2 + y1 y2 = 0. (x2, y2) verifient la relation:
x1 x2 + y1 y2 = 0.
|
|