Maths
- 45 -
Les vecteurs
Partie 1
Partie 2
© The scientific sentence. 2013
|
|
Mathématiques 45: Algèbre vectorielle:
Opérations sur les vecteurs
Somme de deux vecteurs
La somme de deux vecteurs donne un
vecteur résultant appelé résultante.
La somme de vecteurs inclut aussi bien leur
addition que leur soustraction.
La somme de vecteurs se fait par construction
géométrique ou selon les calculs algébriques
sur les composantes des vecteurs.
1. Somme géométrique de deux vecteurs
1.1. Addition géométrique de deux vecteurs
Il existe deux façons de construire géométriquement
la résultante de deux vecteurs: la méthode du
triangle et la méthode du parallélogramme.
1.1.1. méthode du triangle
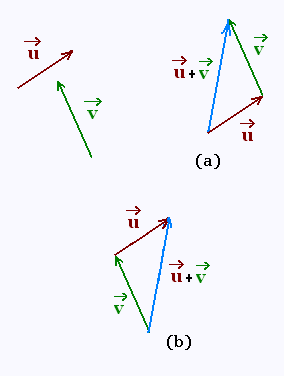 • On prend l’extrémité d’un vecteur et on la place à
l’origine du deuxième vecteur,
• On prend l’extrémité d’un vecteur et on la place à
l’origine du deuxième vecteur,
• Ensuite, on réunit l’origine du premier vecteur à
l’extrémité du deuxième vecteur,
• Le vecteur obtenu est la résulatante cherchée.
On obtient le cas (a) ou le cas (b).
1.1.2. méthode du parallélogramme
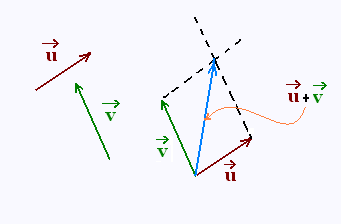
• On place les origines de chacun des vecteurs ensemble,
• On complète le parallélogramme,
• On obtient le vecteur somme en joignant les deux
origines à l'autre sommet du parallélogramme suivant
la dioagonale.
1.2. Soustraction géométrique de deux vecteurs
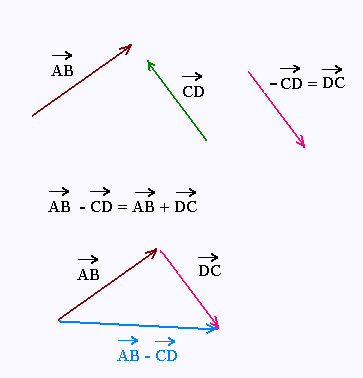
Soustraire un vecteur d'un autre vecteur c'est faire
l'addition du deuxième vecteur et de l'opposé
du premier vecteur.
On transforme d'abord les vecteurs à soustraire en leurs
opposés et ensuite on fait la somme de la même manière
que la somme simple des vecteurs.
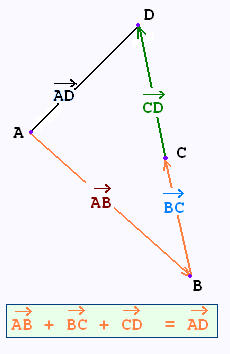
1.3. Relation de Chasles
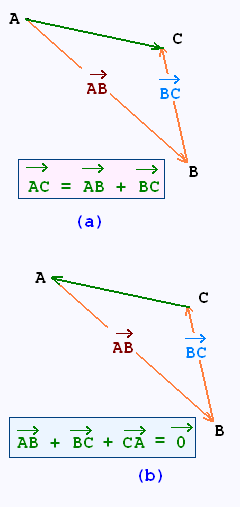
La relation de Chasles est utile pour calculer le vecteur
résultant lorsque l'éxtrémité d'un vecteur coincide avec
l'origine de son suivant.
Dans la relation de chasles, on s'assure que l'origine
du vecteur résultant est la même que l'origine
du premier vecteur, et l'extrémité du vecteur résultant
est la même que celle du dernier vecteur, comme dans
l'égalité suivante:
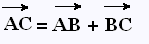
La relation de Chasles peut s'appliquer
dans le cas de plusieurs vecteurs.
Si on fait la somme vectorielle suivant une boucle,
la résultante est le vecteur nul.
2. Somme algébrique de deux vecteurs
La somme de vecteurs inclue aussi bien leur addition
que leur soustraction, car soustaraire des vecteurs
revient à additionner leurs opposés.
2.1. La procédure
Soient deux vecteurs:
 (a1, b1)
et (a1, b1)
et
 (a2, b2) (a2, b2)
Leur somme est:
 + + = (a1 + a2, b1 + b2) = (a1 + a2, b1 + b2)
Leur différence est:
 - - = (a1 - a2, b1 - b2) = (a1 - a2, b1 - b2)
2.2. Exemples
2.2.1. Addition de deux vecteurs
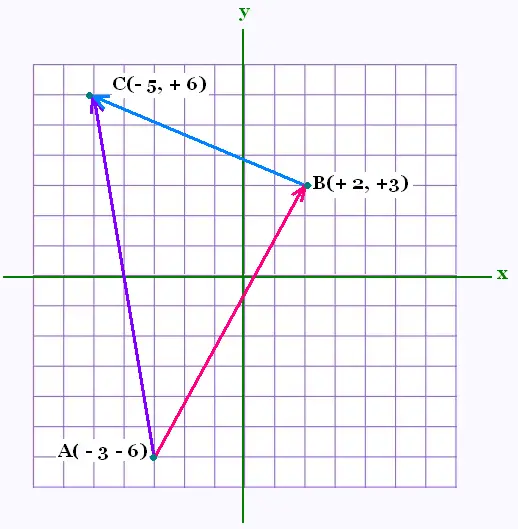
Calculons les composantes de ces trois vecteurs:
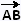 (2 + 3, 3 + 6) = (5, 9) (2 + 3, 3 + 6) = (5, 9)
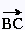 (- 5 - 2, 6 - 3) = (- 7, 3) (- 5 - 2, 6 - 3) = (- 7, 3)
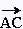 (- 5 + 3, 6 + 6) = (- 2, 12) (- 5 + 3, 6 + 6) = (- 2, 12)
On fait la somme:
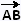 + + 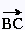 =
(5, 9) + (- 7, 3) = (5 - 7, 9 + 3) = (- 2 , + 12)
= =
(5, 9) + (- 7, 3) = (5 - 7, 9 + 3) = (- 2 , + 12)
= 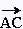
Ainsi:
Additionner deux vecteurs revient à additionner
leurs composantes
2.2.2. Soustraction de deux vecteurs
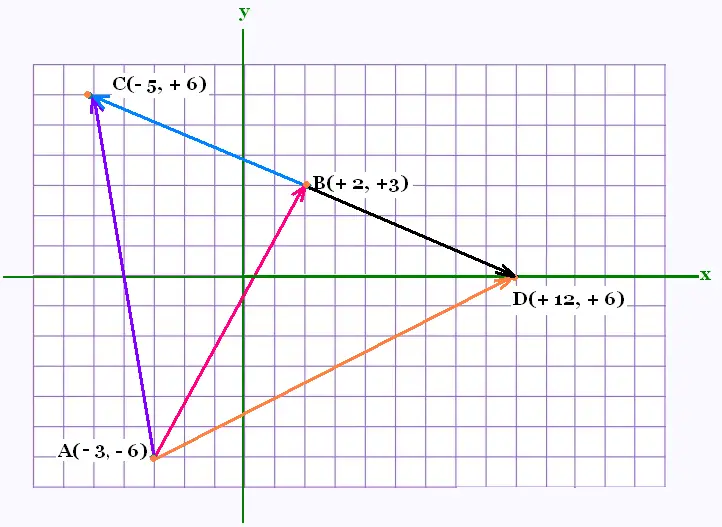
Calculons les composantes des vecteurs:
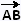 (2 + 3, 3 + 6) = (5, 9) (2 + 3, 3 + 6) = (5, 9)
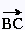 (- 5 - 2, 6 - 3) = (- 7, 3) (- 5 - 2, 6 - 3) = (- 7, 3)
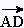 (- 5 + 3, 6 + 6) = (- 2, 12) (- 5 + 3, 6 + 6) = (- 2, 12)
On fait la différence:
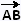 - -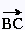 =
(5, 9) - (- 7, 3) = (5, 9) + [- (- 7, 3)] =
=
(5, 9) - (- 7, 3) = (5, 9) + [- (- 7, 3)] =
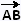 + + 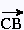 =
(5, 9) + (7, - 3) = (5 + 7, 9 - 3) = (12, + 6)
= =
(5, 9) + (7, - 3) = (5 + 7, 9 - 3) = (12, + 6)
= 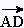
Ainsi:
Soustaraire deux vecteurs revient à soustraire
leurs composantes
|
|