Mécanique
Je confirme mes acquis
Exercices
© The scientific sentence. 2010
|
Mécanique:
Centre de masse
1. Définition
Le centre de masse CM d'un corps est le point situé à la
position moyenne de la masse du corps.
Le CM est essentiellement mathématique. Il peut se trouver sité à l'intérieur
de l'onjet comme à l'extérieur.
Pour un corps homogène, c'est à dire de masse volumique
constante, et parfaitement symétrique, le CM est situé au
centre géométrique du corps. C'est l'exemple
d'une tige, d'une sphère, d'un cylindre ou d'un cube.
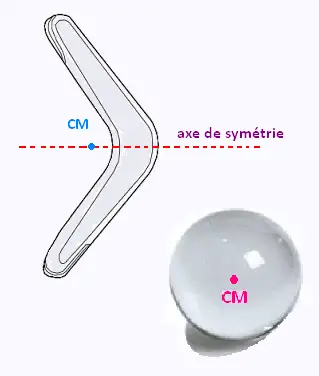
Le centre géométrique d'un corps se trouve sur son axe de symétrie.
Ce n'est pas toujours le centre du corps.
C'est l'exemple d'un boomerang .
En Mécanique, le CM est très important. La trajectoire d'un corps qui meut est en fait
celle de son centre de masse, puisque l'objet est représenté par un point
matériel.
De plus, lorsqu'un corps roule, les points du corps effectuent un
mouvement de rotation autour du centre de masse, tandis que celui-ci
effectue un autre type de mouvement. C'est l'exemple de
la translation du CM d'une boule qui roule horizontalement. .
2. Le CM expériemental

Expérimentalement, on peut determiner la position du centre de masse
d'un corps. On choisit des points différents sur ce corps. Sur chacun de
ces points, on exerce des forces de directions différentes. Lorsque le corps
n'effectue aucune rotation, l'intersection des trois supports de ces forces
localise le centre de masse.
3. La position du centre de masse
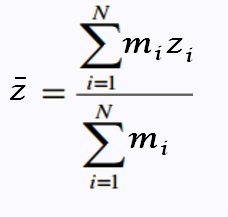
La position du centre de masse est la moyenne pondérée des positions des
masses individuelles qui constituent l'objet.
La moyenne pondérée d'une valeur zi de facteur de pondération mi
est définit par Σmi zi/Σmi :
3.1. Centre de masse d’un système
de deux particules

Où est le centre de masse de ces deux masses?
Nous avons :
m1 = 2 kg
m2 = 6 kg
mtot = m1 + m2 = 2 + 6 = 8 kg.
La position moyenne est donc : xCM = (2 x 0 + 6 x 120)/8 = 90 cm ,
qui est la position du centre de masse des deux boules.
Plus une masse est grande, plus elle rapprochée du CM.
3.2. Centre de masse d’un système de
plusieurs particules en deux dimensions
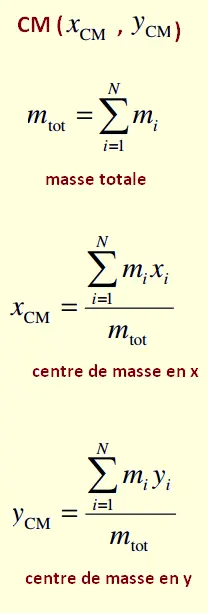
De façon générale, le CM d'un système de N particules
se calcule au moyen des formules ci-contre:
• xCM : Position du centre de masse selon l'axe x (m)
• yCM : Position du centre de masse selon l'axe y (m)
• mi : La masse de la particule i (kg), c'est le coefficient de pondération
• xi : La position selon l'axe x de la particule i (m)
• yi : La position selon l’axe y de la particule i (m)
• N : Le nombre de particules qui constituent l'objet
• mtot : La masse totale des particules du système (kg)
Exemple: Système de quatre masses
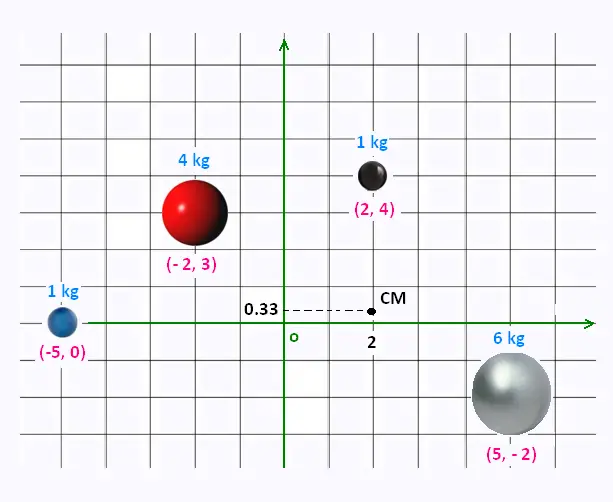
Où est le centre de masse de ces deux masses?
Nous avons :
m1 = 1 kg, m2 = 4 kg, m3 = 1 kg, m2 = 6 kg
mtot = m1 + m2 + m3 + m4 = 1 +
4 + 1 + 6 = 12 kg.
xCM = (1 x - 5 + 4 x - 2 + 1 x 2 + 6 x 5)/12 =
24/12 = 2 unités,
yCM = (1 x 0 + 4 x 3 + 1 x 4 + 6 x - 2)/12 = 4/12 = 1/3 = 0.33
= 1/3 unité,
xCM = 2
yCM = 1/3
qui est la position du centre de masse des quatre boules.
4. CM et densité de masse
4.1. Densité de masse
La densité de masse est la mesure de la masse moyenne par unité de
dimension. La dimension est la longueur L, ou la surface A ou de volume V.
On distingue:
• Densité linéaire de masse : μ en kg/m
• Densité surfacique de masse : σ en kg/m2
• Densité volumique de masse : ρ en kg/m3
Connaissant la densité de masse et la dimension d'un objet, on peut donc
évaluer sa masse totale grâce aux équations suivantes :
• Masse d'une longueur : m = μ x L
• Masse d'une surface : m = σ x A
• Masse d'un volume : m = ρ x V
où
m : Masse du corps homogène (kg)
L : Longueur du corps (m)
A : Aire du corps (m2)
V : Volume du corps (m3)
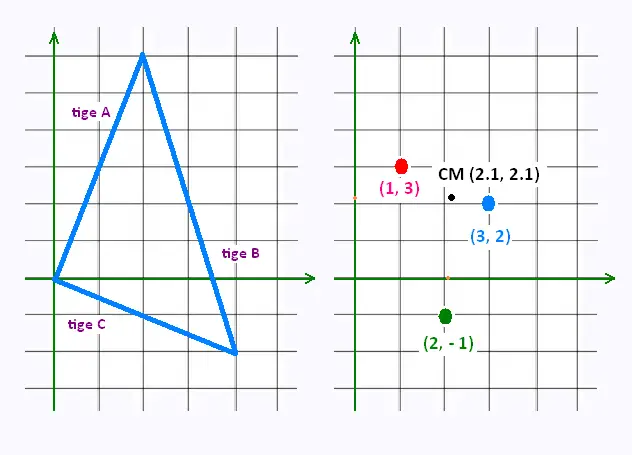
4.2. Exemple: triangle métallique
On dispose d'un fil de métal homogène, de section uniforme, et
de densité linéaire de masse μ. On plie ce fil afin de former
un triangle représenté ci-contre.
On désire déterminer les coordonnées du centre de masse du triangle.
On découpe le triangle formé en trois tiges. On calcule la masse de chaque tige,
puis on évalue son centre de masse. La tige est alors équivalente à une masse
ponctuelle située au CN calculé.
Les tiges sont homogènes, le centre de masse de chaque tige
est donc au centre géométrique de la tige:
a) Tige A
• Longueur LA = √(4 + 36) = 2√10
• masse mA = μ LA = 2μ√10
• xACM = 1
• yACM = 3
b) Tige B
• Longueur LB = √(4 + 64) = 2√17
• masse mB = μ LB = 2μ√17
• xBCM = 3
• yBCM = 2
c) Tige C
• Longueur LC = √(4 + 16) = 2√5
• masse mC = μ LC = 2μ√5
• xCCM = 2
• yCCM = - 1
Masse totale = mtot = 2μ(√10 + √17 + √5) = 19.04 μ
Avec i = A, B, C, on a donc:
xCM = Σximi
= (mA xACM +
mB xBCM +
mC xCCM )/mtot
yCM = Σyimi
= (mA yACM +
mB yBCM +
mC yCCM )/mtot
xCM = (1 x 2μ√10 + 3 x 2μ√17 + 2 x 2μ√5)/mtot =
2μ(√10 + 3√17 + 2√5)/2μ(√10 + √17 + √5)=
= 2.1
yCM = (3 x 2μ√10 + 2 x 2μ√17 + 1 x 2μ√5)/mtot =
2μ(3√10 + 2√17 + √5)/2μ(√10 + √17 + √5)
= 2.1
CM(2.1, 2.1)
5. CM et masse négative
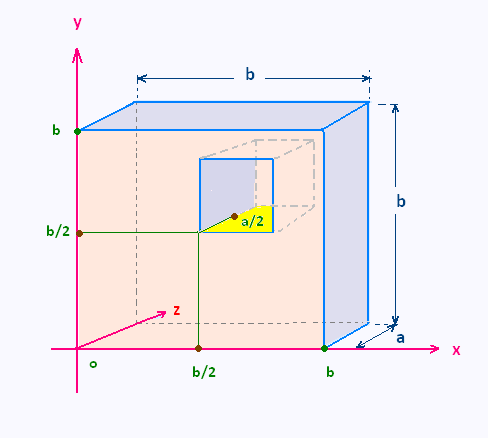
On considère un prisme homogène à base carrée de côté b et d'épaisseur a.
Dans ce prisme, on perce un petit prisme de dimensions a.
• Prisme plein:
Le CM du prisme plein est le centre de ce prisme CMP:
xCMP = b/2
yCMP = b/2
zCMP = a/2
Masse du prisme plein mP = ρ ab2.
• Petit prisme vide:
Le CM du petit prisme vide est le centre de ce prisme CMV:
xCMV = b/2 + a/2 = (a + b)/2
yCMV = b/2 + a/2 = (a + b)/2
zCMV = a/2
La masse du petit prisme vide mV = - ρ a3
• Prisme troué:
La masse totale du système est la masse du prisme troué = mT =
mP + mV =
ρ ab2 - ρ a3 = ρ(ab2 - a3)
Le CM du prisme troué CM se calcule selon les formules:
xCM = [mP b/2 + mV (a + b)/2]/mT =
[ρ ab2 b/2 - ρ a3(a + b)/2]/ρ(ab2 - a3) =
[b3 - a2(a + b)]/2(b2 - a2)
xCM = [b3 - a2(a + b)]/2(b2 - a2)
yCM = [mP b/2 + mV (a + b)/2]/mT =
[b3 - a2(a + b)]/2(b2 - a2)
yCM = [b3 - a2(a + b)]/2(b2 - a2)
zCM = [mP a/2 + mV a/2]/mT =
(a/2)[ρ ab2 - ρ a3 ]/ ρ(ab2 - a3) =
a/2
zCM = a/2
CM([b3 - a2(a + b)]/2(b2 - a2),
[b3 - a2(a + b)]/2(b2 - a2) , a/2)
Exemple:
a = 1 unité
b = 3 unités
CM(23/16, 23/16, 1/2)
6. Le centre de masse par intégration
Dans le cas où c'est possible de différentier la masse, l'intégrale
est pratique pour calculer les coordonnées du CM d'un corps de mase totale
mtot:
xCM = (1/mtot)∫ x dm ,
yCM = (1/mtot)∫ y dm , et
zCM = (1/mtot)∫ z dm .
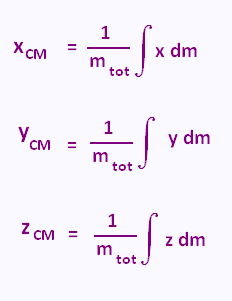
|
|