Dynamics: Frictions within two blocks
Newton's law applications
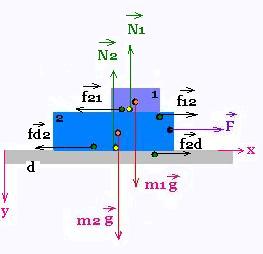
N1: is the normal force regarding the mass m1,
N2: is the normal force regarding the mass m2,
F: is the force with which we move the block of the two masses,
a: is the acceleration of the system ( block = m1 + m2),
a1: is the acceleration of the mass m1,
a2: is the acceleration of the mass m2,
f12: is the friction force of the body 1 on the body 2,
f21: is the friction force of the body 2 on the body 1,
fd2: is the friction force of the desk on the body 2,
f2d: is the friction force of body 2 on the desk,
μs and μk: are the static and kinetic
friction coefficient respectively,
g: is the acceleration of gravity.
The two bodies of the system are made up from the same substance.
1. The condition to move the block:
The condition to move the block (m1 + m2)
by exerting the force F is:
F > fd2. That is:
F > μs(m1 + m2)g
or
μs < F/(m1 + m2)g
μs < F/(m1 + m2)g
(1)
2. The expressions of the friction forces:
They are:
f21 = μsm1g
fd2 = μk(m1 + m2)g
f21 = μsm1g
fd2 = μk(m1 + m2)g
(2)
3. The acceleration of the entire block:
The acceleration of the block is:
a = (F - fd2 )/(m1 + m2) = [F - μk(m1 + m2)g]/(m1 + m2)
a = [F - μk(m1 + m2)g]/(m1 + m2)
(3)
4. The acceleration of the part m1 moving at right:
The acceleration of the part m1 is:
a1 = - f21/m1 = - [μkm1g]/m1 = - μkg
a1 = - μkg
(4)
5. The acceleration of the part m2:
1. While the part m1 is moving right:
The acceleration of the part m2 is:
F + f12 - fd2 = m2 a2
a2 = (F + f12 - fd2)/m2 =
[F + μk m1 g - (μk (m1 + m2) g )]/m2
=[F + μk m1 g - μkm1g - μk m2 g]/m2
= [F - μk m2 g ]/m2
2. While the part m1 is moving left:
The acceleration of the part m2 is:
F - f12 - fd2 = m2 a2
a2 = (F - f12 - fd2)/m2 =
[F - μk m1 g - (μk (m1 + m2) g )]/m2
= [F - μk m1 g - μkm1g - μk m2 g]/m2
= [F - 2 μk m1 g - μk m2 g ]/m2
= [F - μk (2 m1 + m2]g/m2
The part m1 is moving right:
a = [F - μk m2 g ]/m2
The part m1 is moving left:
a = [F - μk (2 m1 + m2]g/m2
(5)
6. The condition for that m1 remains stick on m2 :
This condition is satisfied when:
m1 a >= f21, a is the acceleration of
the entire block 1 and 2 (formula (3)).
That is :
m1 a >= μkm1g
or
a/g >= μk
That is:
2 μk <= F/g(m1 + m2)
Finally,
μk <= F/2g(m1 + m2)
μk <= F/2g(m1 + m2)
(6)
7. The condition for that m1 moves backward :
The part1 will move backward if m1a < f21
that is:
μk > F/2g(m1 + m2)
μk > F/2g(m1 + m2)
(7)
8. Applications:
F = 30 Newtons
M1 = 2 kg
M1 = 4 Kg
What would be the values of μs and μk
for the system to have different situations?
1.
The condition (1) is then:
μs < F/(m1 + m2)g
μs < 30/60 = 0.5
With any blocks of the friction coefficient greater than
0.5, the force F = 30 N will not move it.
a = a1 = a2= 0
2.
μs = 0.4
The system can move.
with a related μk= 0.3
The condition (7) is :
μk > F/2g(m1 + m2)
F/2g(m1 + m2 = 30/20x6 = 1/4 = 0.25
The answer is yes. Hence:
m1 will move backward.
From the relationship (4), we have:
a1 = [μkm1g]/m1 = μkg = 3 m/s2
From the relationship (5), we have:
a2 = [F - μkg(2m1 + m2]/m2
= 30 - 0.3 x 10 ( 2 x 2 + 4)/4 = (30 - 24 )/4 = 6/4 = 3/2 = 1.5 m/s2
3.
μk = 0.1
The relationship (6) gives the threshold:
μk = F/2g(m1 + m2)= 30/20x6 = 0.25
μk = 0.1 < 0.25,
then the two parts m1 and m2
will remains stick and move together with the following accelerations:
a1 = μkg = 0.1 x 10 = 1.0 m/s2
a2 = [F - μkg(2m1 + m2]/m2
= 30 - 0.1 x 10 ( 2 x 2 + 4)/4 = 30 - 1.0 x 8 /4 = 22/4 = 11/2
= 5.5 m/s2.
4.
μk = 0
μk = 0 < 0.25,
then the two parts m1 and m2
will remains stick and move together with the following acceleration (given
by the relationship (3) with μk = 0):
a = F/(m1 + m2) = 30 /6 = 5 m/s2.
|