Dynamics: Inclined plane
Newton's law applications

1. Simple inclined plane

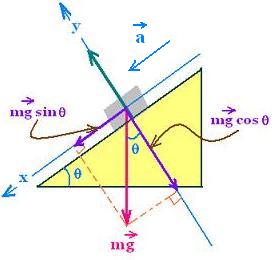
Why do we use a ramp to load a car into the back of a truck?

We use a ramp to make the task easier.

The inclined plane is a flat surface whose endpoints are at different heights. By moving an object up an inclined plane rather than directly from one height to another, we make the task easier.

The inclined plan is a machine. A machine is any device that transmits or modifies force applying to an object.
All machines are combinations or modifications of six fundamental types of machines, called simple machines

There are two forces acting on the body (neglecting friction and air resistance) sliding on the inclined plane:

1. N = Normal force that is perpendicular to the plane. It is exerted by the plane onto the body of mass m,

2. m g = The weight of the object acting vertically downwards, g = acceleration due to gravity.

The gravitational force is replaced by its two components:
A force parallel to the plane mg sin θ, and a force acting into the plane mg cos θ which is equal and opposite to N.
θ = angle of elevation of the plane, measured from the horizontal.

Newton's second law written along y axis gives:
N - mg cos θ = ma_y = 0

And along the x-axis gives:
m g sin θ = ma _x = m a

Therefore:
a = g sin θ

a = g sin θ

2. Double inclined plane

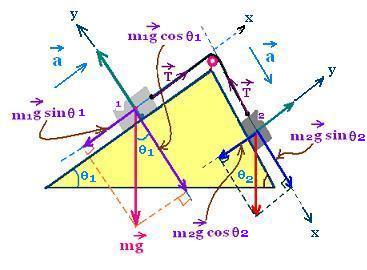
Two blocks (1) and (2) connected by an inextensible string passing over a frictionless pulley fixed at the top of a double inclined plane.

The tension on the blok (1) T1 is equal to the tension T2 on the block (2) because the string is inextensible and the pulley is frictionless. We have:
T1 = T2 = T (in magnitude)

There two cases:

case 1:

The the block (1) of masse m1 move up along the incline plane of angle of inclination θ1, and the block (2) of masse m2 move down the inclined plane of angle θ2.

Newton's second law for (1) and (2) gives:

For (1): T - m1 g sin θ1 = m1 a    (1)
For (2): - T + m2 g sin θ2 = m1 a    (2)

Adding (1) and (2), gives:
g(m2 sin θ2 - m1 sin θ1) = (m1 + m2) a
or

a = g(m2 sin θ2 - m1 sin θ1) /(m1 + m2))

Replacing this expression in (1) gives an expression of the tension:
T = m1 g sin θ1 + m1 a = m1 (g sin θ1 + a) =
m1 g [ sin θ1 + (m2 sin θ2 - m1 sin θ1) /(m1 + m2))] =
[m1 g /(m1 + m2))][ m1 sin θ1 + m2 sin θ1 + m2 sin θ2 - m1 sin θ1] =
m1 m2 g (sin θ1 + sin θ2)/(m1 + m2)

a = g(m2sinθ2 - m1sinθ1)/(m1+m2)

T = m1 (g sin θ1 + a)


case 2:

The the block (1) of masse m1 move down along the incline plane of angle of inclination θ1, and the block (2) of masse m2 move up the inclined plane of angle θ2.

Newton's second law for (1) and (2) gives:
For (1): T - m1 g sin θ1 = m1 (- a)    (1)
For (2): - T + m2 g sin θ2 = m1 (- a)    (2)


Adding (1) and (2), gives:
g(m2 sin θ2 - m1 sin θ1) = - (m1 + m2) a
or

a = g(m1 sin θ1 - m2 sin θ2) /(m1 + m2))

Replacing this expression in (1) gives an expression of the tension:
T = m1 g sin θ1 - m1 a = m1 (g sin θ1 - a) =
m1 g [ sin θ1 + (m2 sin θ2 - m1 sin θ1) /(m1 + m2)] =
[m1 g /(m1 + m2)][ m1 sin θ1 + m2 sin θ1 + m2 sin θ2 - m1 sin θ1] =
m1 m2 g (sin θ1 + sin θ2)/(m1 + m2) (sane value as before)

a = g(m1sinθ1 - m2sin θ2)/(m1+m2)

T = m1 (g sin θ1 - a)



Conclusion:

If g(m2 sin θ2 - m1 sin θ1) > 0 , that is : m2 sin θ2 > m1 sin θ1, the motion is clockwise (m2 down and m1 up)

If g(m1 sin θ1 - m2 sin θ2) > 0 , that is : m1 sin θ1 > m2 sin θ2, the motion is counterclockwise (m1 down and m2 up).

3. Direction of motion

The rule about the orientation of the axes is:


1. Orient the vector acceleration a in the same positive direction of the axis,
2. Do related calculations and find the magnitude a of the the vector acceleration,
3. If a is positive, the chosen direction is true, then the object is really moving in that direction,
4. If a is negative, the chosen direction is false, then the object is moving in the opposite direction.

4. Particular cases

4.1. θ2 = 90^o:

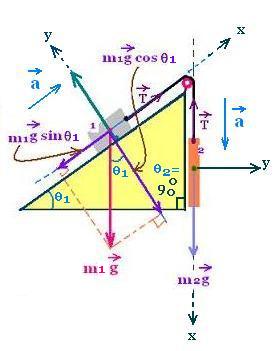
The above formula become:

a = g(m1sinθ1 - m2sin 90^o)/(m1+m2) =
g(m1sinθ1 - m2)/(m1+m2)

T = m1 (g sin θ1 - a)

a = = g(m1 sin θ1 - m2)/(m1+m2)

T = m1 (g sin θ1 - a)

4.2. θ1 = 0^o:

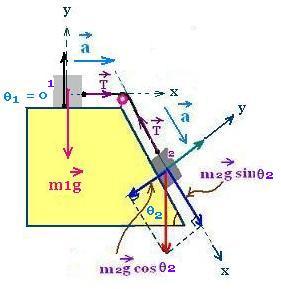
The above formula become:

a = g(m2sinθ2 - m1sinθ0)/(m1+m2) =
g(m2sin θ2)/(m1+m2)

T = m1 (g sin 0 + a) = m1 a

a = g(m2sin θ2)/(m1+m2)

T = m1 a

The magnitude of the acceleration a is positive, the chosen direction is true, then the object is really moving in that direction.

4.3. θ1 = 90^o and θ2 = 90^o:

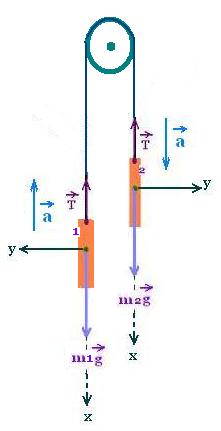
The above formula become:

a = g(m2sin 90^o - m1sin 90^o)/(m1+m2) =
= g (m2 - m1)/(m1+m2)

T = m1 (g sin 90^o + a) = T = m1 (g + a)

a = g (m2 - m1)/(m1+m2)

T = m1 (g + a)

The magnitude of the acceleration a is positive if m2 is greater than m1, corresponding to the chosen direction, otherwise (if m2 < m1), the system will move in the opposite directon.

4.4. θ1 = 0^o and θ2 = 0^o:

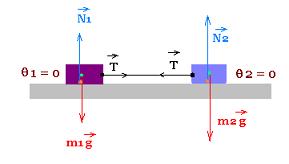
The above formula become:

a = g(m2sin 0^o - m1sin 0^o)/(m1+m2) = 0


T = m1 (g sin 0^o + a) = T = m1 a

a = 0

T = m1 a

The magnitude of the acceleration a is zero. The system could be at rest or at constante speed.