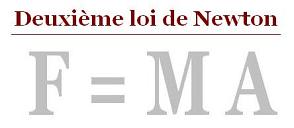
1. Première loi de Newton ou principe de l'inertie:

Voici le principe:

Tout corps conserve son état de repos ou de mouvement rectiligne uniforme, à moins que des forces externes ayant une résultante non nulle n'agissent sur lui et ne le contraignent à changer d'état de mouvement.

Si cette force agit sur l'objet, elle produit une accélération de l'objet au moyen de la variation de sa vitesse.

Naturellement, tout corps a une tendence de résister à toute variation de son état de mouvement. Cette tendence est appelée inertie. La mesure de cette inertie est appelée masse de l'objet.

Un repère de référence est appelé référentiel inertiel ou galiléen, si dans ce repère, le principe de l'inertie est verifié.

Le principe de l'inertie affirme l'existence des référentiels galiléens. Il ne fait intervenir aucune relation fonctionnelle entre la force et l'accélération. C'est la deuxième loi qui le fait.

2. Deuxième loi de Newton ou principe fondamental de la dynamique:

Pour determiner comment l'accélération dépend de la force, en faisant intervenir la masse, nous allons faire varier ses grandeurs séparement:

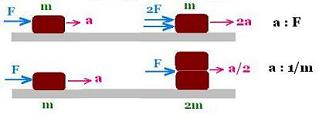
-- Si la masse est maintunue constante, alors que la force varie, il apparait que a α F
-- Si la force est gardée constante, tandis que la masse varie, il apparait que a α 1/m

Donc a α F/m, ou bien F α a x m; et l'on peut ecrire:
F = k x a x m, où k est la constante de proportionnalité.

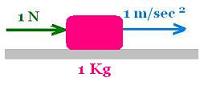
On determine la constante k en utilisant les unités:
Dans le system d'unités SI, une force de 1 Newton appliquée à une masse de i Kg produit une accélération de 1 m/s².
Donc k = 1.
La formule obtenue s'ecrit:
F = m x a.

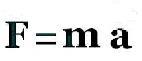
Lorsque plusieurs forces F agissent sur une particule, on doit calculer leur somme vectorielle , ainsi la deuxième loi de Newton s'ecrit:
ΣF = m a.

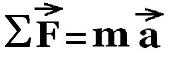
La force résultante agissant sur un object lui procure une accélération de même direction. Cette accélération doit être mesurée dand un référentiel inertiel.

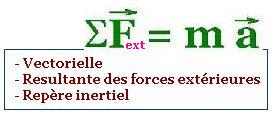
3. Exemples

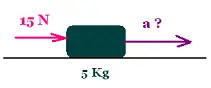
3.1. Exemple 1

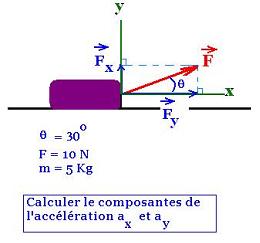
3.2. Exemple 2