Physics
Mechanics
Pulleys

The pulley used in Mechnaics is assumed to be smooth and light. That is we neglect its friction and its mass.

The connecting string is generally taken to be light and inextensible.

The magnitude of the tension throughout the string is the same.

In addition, the acceleration of each particle, on either side of the pulley, is of the same magnitude, but in opposite directions.

Exercise 1

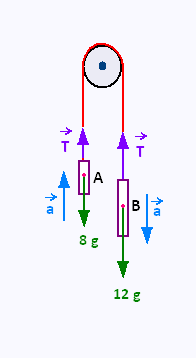
A light inextensible string passes over a smooth light pulley.

At each end of the string there is a particle. Particle A has a mass of 10 kg and particle B has a mass of 12 kg as shown in the diagram.

The two particles are released from rest with the string taut. Calculate the tension in the string and the acceleration of the masses.

Solution

It is it is practical and usual to consider each of the particles separately and drawing a free body diagram for each particle.

Using Newton’s second law, F = m a, on particle A, in the direction of motion (↑), gives:

T - 8 g = 8 a (1)

Using Newton’s second law, F = ma, on particle B, in the direction of motion (↓), gives:

12 g - T = 12 a (2)

Now, we solve the simultaneous equations (1) and (2).

From (1): T = 8a + 8g (3)

Substituting (3) into (2) gives:

12 g - 8a - 8g = 12 a

4g = 20a ⇒ a = 4g/20 = g/5 = 0.2 g = 0.2 x 9.8 = 1.96 m.s^{- 2}

a = 1.96 m.s^{- 2}

Now, we substitute this value into one of the equations, say (3), to obtain

T = 8 x (g/5) + 8g = 8g (1 + 1/5) = 48g/5 = 48 x 9.8/5 = 94.08

T = 94.08 N

Exercise 2

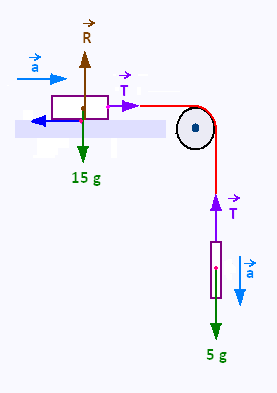
A box, of mass 15 kg, is sliding along a rough horizontal table. It is connected to another box of mass 5 kg, via a light inextensible string, which passes over a smooth light pulley (as shown in the diagram).

Given that the coefficient of sliding friction between the table and the box is 0.2, what is the acceleration of each particle and what is the tension in the string?

Solution

Firstly consider the box on the table. The magnitude of the normal reaction, R, is equal to the magnitude of the weight of the box, 15g.

As the box is sliding:

Friction = Fr = µR = 0.2 x 15 g = 3g

Applying Newton’s second law, F = ma, on this box in the direction of motion (→), gives:

T - Fr = 15a

T - 3g = 15 a (1)

Applying Newton’s second law, F = ma, to the hanging box in the direction of motion (↓), gives:

5g - T = 5a (2)

Rearranging (1) gives: T = 3 g + 15 a (3)

Substituting into (2) gives: 5g - 3g - 15 a = 5a

2g = 20 a ⇒ a = 2g/20 = 0.1 g

a = 0.98 m.s^{- 2}

Substituting this back into one of the equations, say (3) gives:

T = 3 g + 15 g/10 = 4.5 g = 44.10

T = 44.10 N