Dynamics
Contents
Applications
Exercises
© The scientific sentence. 2010
| Dynamics: Skater on icy road
1. Definitions
Let's recall:
1. A friction force ƒ on a moving object, is equal to the kinetic
friction coefficient μk times the
normal force. If the normal force equates the weight mg, then:
N = mg and ƒ = μk N = μk m g.
2. The friction force is a non-conservative force. The work
done by this force is always negative.
3. The work done by a conservative force (such as gravitational
force) on a moving object does not depend on the path
taken by this object. It depends only on the initial
and final position of the object.
4. The work done by any force F on a moving object is equal to
the scalar product of this force by the displacement l
of the object:
W = (vector)F . (vector)l = F l cos θ.
θ is the angle between the two vectors F and l.
Therefore
The force normal to the displacement does not work. The only
forces that work are parallel to the displacement.
5. The kinetic energy theorem holds for the conservative forces
and for the non-conservative forces.
It is written as:
ΔKE = Σ W(Fext)
Δ KE is the difference between the final
kinetic energy and the initial kinetic energy of the
object of mass m:
= (1/2) m vf2 - (1/2) m vi2
Where
vi and vf are the initial and final
velocities of the object respectively.
W(Fext) is the work done by all the external forces
that act on the object(such as gravitational force, normal
force, friction force, ...)
6. The energy conservation principle holds for only
for the conservative forces. It says: The total (or mechanical) energy
E of a system, which is equal to the sum of the kinetic
energy KE and the potential energy PE is conserved.
It is written as:
E = KE + PE = constant, or
KEinitial + PEinitial = KEfinal + PEfinal
1. Skater on icy road
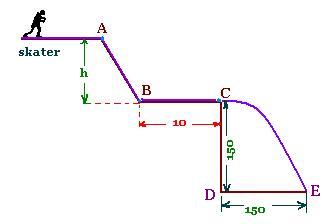
1. Part CE
At the point C, the skater has an horizontal
velocity vC.
The height (CD) is written as
(CD) = (1/2) g t2
The horizontal range (DE) is written as
(DE) = vC t
Therefore
vC = (DE)/t
Squaring gives:
vC2 = (DE)2/t2
Substituting "t" given by the first relationship, we get:
vC2 = g (DE)2/2(CD) (1)
2. Part BC
Applying the Kinetic energy theorem from B to C yields:
(1/2) m [vC2 - vB2]
= (Ff) (xC - xB)
= - (m g μk)(BC)
Therefore
(1/2) [vC2 - vB2] =
- (g μk)(BC)
Hence
vB2 = vC2 + (2g μk)(BC)
(2)
Remark:
We can use here the Kinematics formula:
vc2 - vB2 =
2 a (xC - xB)
Where "a" is the acceleration of the skater given by Newton's second
law:
Σ F = m a.
We have: Σ F = Friction force = - ƒ ( minus sign because
it is directed in the opposite side of the acceleration, which is the
direction of the motion). Therefore
m a = - ƒ = - m g μk. So
a = - g μk.
Substituting "a" in the above Kinematic formula gives:
vc2 - vB2 =
- 2 g μk (xC - xB)
That is:
vc2 + 2 g μk (BC) = vB2,
Which is exactly the same found formula (2)
3. Part AB
Applying the Kinetic energy theorem from A to B,
along the incline plane yields:
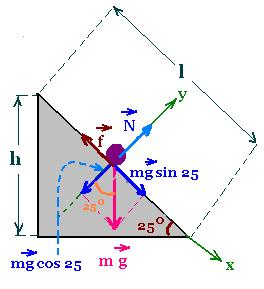
ΔKE = Σ Work(Fext)
The Fext are: mg, N, and ƒ
N does not work.
The net force that works is
m g sin 25 - ƒ =
m g sin 25 - μk m g cos 25.
This net force does a work over the inclined distance "l". This work
is:
[m g sin 25 - μk m g cos 25] l.
Therefore
(1/2) m[vB2 - 0 ] = [m g sin 25 - μk m g cos 25] l
with h/l = sin 25,
that is l = h/sin 25, we get:
[vB2 = 2 [ g sin 25 - μk g cos 25] (h/sin 25)
[vB2 = 2 g [sin 25 - μk cos 25] (h/sin 25)
or
vB2 = 2 g h [1 - μk cot 25]
(3)
Recall: cot θ = 1/tan θ = cos θ /sin θ
4. Rearranging the above results:
Using (2) gives:
vC2 + (2g μk)(BC) =
2 g h [1 - μk cot 25]
Using (1), gives:
g (DE)2/2(CD) = - (2g μk)(BC) +
2 g h [1 - μk cot 25]
[g (DE)2/2(CD) + (2g μk)(BC)] =
2 g h [1 - μk cot 25]
h = [g (DE)2/2(CD) + (2g μk)(BC)] /
2 g [1 - μk cot 25]
We have:
CD = DE = 1.50
Then
h = [(DE)/4 + (μk)(BC)] /
[1 - μk cot 25]
With
BC = 10 m
μk = 0.402
h = [(1.50)/4 + (0.402)(10)] /
[1 - 0.402 cotg 25]
= (0.375 + 4.02)/(1 - 0.862) = 31.85 m
h = 31.85 m
h = 31.85 meters
|
|