Dynamics
Contents
Applications
Exercises
© The scientific sentence. 2010
| Dynamics: Work energy applications
Recall that centripetal force is provided by another force.
1. Sled sliding on frictionless surface
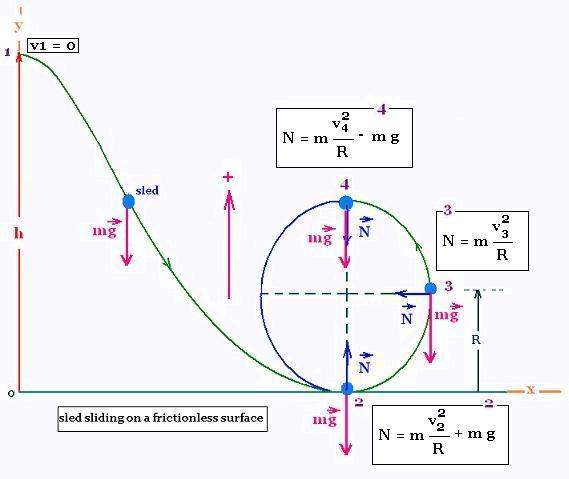
Let's consider a sled starting from from rest (v1 = 0) at the top of an icy hill.
The path from 1 to 2 is circular with radius R, that we assume uniform. We neglect
frictions. We want to determine the speeds of the sled and the normal forces
exerted by the ice on it at the points 2, 3, and 4.
We recall that centripetal force is provided by amother force.
Here it provides the resultant N + W, that is the normal force exerted by the ice
on the sled + the weight W = mg of the sled. Further, we apply the work-energy theorem.
(1/2)m(vf2 - vi2) = - mg (xf - xi)
1. At the point 1:
v1 = 0
1. At the point 2:
(1/2) m (v22 - v12) = - mg (0 - h)
(1/2) m v22 = mgh
v2 = [2gh]1/2
v2 = [2gh]1/2
The second Newton's law is written as:
W + N provides centripetal force = Fc
This force is radial, then oriented toward the center of the circle.
Therefore:
The vector relationship is:
N + W = Fc
Their components along + y-axis gives:
+ N - mg = + Fc, that is:
N - mg = mv22/R, Thus:
N = mg + mv22/R
N = mg + mv22/R
At the point 2:
v2 = [2gh]1/2
N = mg + mv22/R
1. At the point 3:
At this point, the component of the weight is zero
along the x-axis, so
N = Fc, that is:
N = mv32/R
N = mv32/R
Applying the work-energy theorem gives:
(1/2) m (v32 - v22) = - mg (R - 0)
(1/2) m (v32 - v22) = - mgR
v32 = - 2gR + v22
Since v22 = 2gh, we have:
v32 = 2gh - 2gR
v32 = 2gh - 2gR
At the point 3:
v3 = [2gh - 2gR]1/2
N = mv32/R
1. At the point 4:
The vector relationship is:
N + W = Fc
Their components along + y-axis gives:
- N - mg = - Fc, that is N + mg = Fc, or
N + mg = mv42/R, Thus:
N = mv42/R - mg
N = mv42/R - mg
Applying the work-energy theorem
(between the two points 4 and 2) gives:
(1/2) m (v42 - v22) = - mg (2R - 0)
or
(v42 - v22) = - 4Rg
v42 = v22 - 4Rg
Since v22 = 2gh, we have:
v42 = 2gh - 4Rg
v4 = (2gh - 4Rg)1/2
At the point 4:
v4 = (2gh - 4Rg)1/2
N = mv42/R - mg
At this point, to still have contact between the sled and the
circular support, we must have N > 0, that is:
mv42/R - mg > 0 or
v42 > Rg
That is:
h > 5R/2
At the top (the point 4), to still have
contact, the height h must satisfy:
h > 5R/2
|
|