Dynamics: Conservation of energy
Conservative force
Work Energy theorem
1.Work done by a force
The work done by an acting force is egal to the product of this
force by the distance travelled.
More precisely:
dot product of the force by the vector distance travelled.
W = (vector force) . (vector distance)
Work is a scalar.
The SI units of work are Joules (J) (1 Joule = 1 Newton . meter).
In cgs units: 1 erg = 1 dyne . cm.
2.Conservative force
A force is conservative if its work done is independent of the taken path.
It depends only on the initial position and the final position.
Equivalently, the net work done in a closed loop is zero.
If a force is conservative, it corresponds to it a potential energy.
The force changes its the potential energy. It derives from a potential.
The force is the rate change of its potential energy with
respect to the traveling distance.
If the force is not conservative (or dissipative), then its work done is
dependent of the taken path , and defining a potential to it is not possible.
Gravity and string forces are two examples of a conservative force,
while friction and air resistance are examples of a non-conservative
force.
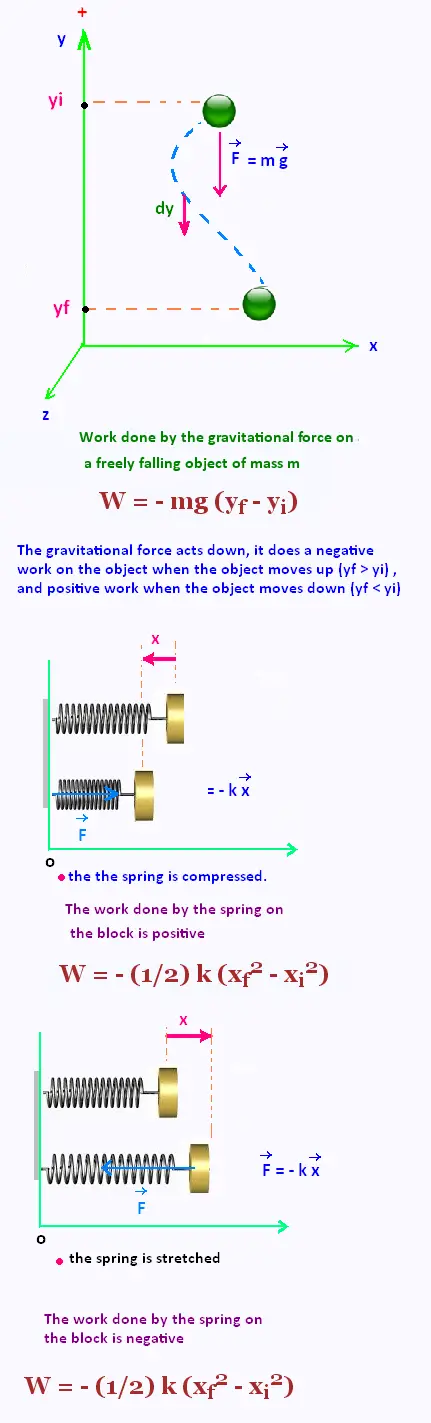
3. Potential Energy
The potential energy stored in a spring is PEs = (1/2) k x2 .
We usually define xi = 0 and xf = x which gives the restoring
force : Fs = - kx, which is called Hooke's law.
F(x = 0 to x) --> Average force (F(0) + F(x)/2 = (0 + kx2)/2
= kx2/2
3.1. Gravitational Potential Energy
Gravitational Potential Energy (PEg )is given by:
PEg = mgy
where m is the mass of an object, g is the acceleration due to gravity,
and y is the distance the object is above some reference level
Potential energy and kinetic energy are different aspects of the
same thing (mechanical energy).
Kinetic Energy ( KE ) (energy of motion)
Potential Energy ( PE ) (energy of position)
3.2. Kinetic energy
The kinetic energy (KE ) of an object of mass m that is moving
with velocity v is:
KE = (1/2) m v2
4. The work-energy theorem
Δ KE = KEf - KEi = W
Proof:
The kinematic relations are:
a = dv/dt (1)
v(t) = at + vo (2)
x (t) = xo + v0t + (1/2) at2 (3)
Eliminating t from (2) and (3) gives:
v2 - vo2 = 2a (x - x0) (4)
x - x0 = (1/2)(v + vo)t (5)
So, multiplying by (1/2) m the both side of the relation (4), yields:
Δ KE = (1/2)m (v2 - vo2) = a m (x - x0) = W
5. The Conservative laws
5.1. Conservative Forces and
the Work-Energy Theorem
The work done by an external force is not always stored as some form of
potential energy. This is only true if the force is conservative:
Wc = Fcext(xB - xA) = PEA - PEB.
5.2. The Conservation of Mechanical Energy:
Mechanical energy is the kinetic energy plus all of the kinds of
potential energy that are present. In the absence of non-conservative
forces, mechanical energy is conserved.
Example:
If gravitational and spring forces are present:
KEi + PEgi + PEsi = KEf + PEgf + PEsf.
5.3. Non-Conservative Forces and
the Work-Energy Theorem :
If there are non-conservative forces, then mechanical energy is not
conserved. We write, the new work-energy theorem
Δ KE = KEf - KEi = W = Wnc + Wc
where Wc is the work done by conservative forces and Wnc is the work
done by non-conservative forces.
Since Wc = PEi - PEf we have:
Wnc = (KEf - KEi) + (PEf - PEi).
The work done by non-conservative forces is equal to the change
in mechanical energy.
6. Power :
Power is the time rate of doing work or, the amount of work done
per second.
Average Power p = W/δt = F . (Δs/Δt) =
F . v
where Δ is the time interval in which the work is done.
Instantaneous Power:
P = Fv.
Power is a scalar.
SI Units: 1 Watt (W) = 1 Joule/sec = 1 kg m2/s3
British Engineering Units: 1 horsepower (hp ) = 746 W .
7. Reminders on the gravitational force
and the string force
|