Dynamics
Contents
Applications
Exercises
© The scientific sentence. 2010
|
Dynamics: Work energy
Given an initial position and velocity of
a particle, we can then solve for its motion
at any instant.
1. Work done by a constant force
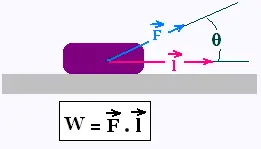 A constant force F is acting on an object that causes it to moves
on a straight line. The object undergoes a displacement Δr = l.
A constant force F is acting on an object that causes it to moves
on a straight line. The object undergoes a displacement Δr = l.
The work
done by the force is defined as a dot product of the two vectors
F and l:
w = F.l = |F| |l| cos θ
Where θ is the angle between l and F.
Δr = l is the displacement from a point to another.
The SI unit is the Joule (J) = N m = kg m2/s2
Work done by force F on object along the displacement l:
W = F.l = Fl cos(F,l)
Notice that the work is done when the object moves.
It is zero when F is zero or l is zero. Then, even though if one
exerts a force (pushes) against a wall (immobile object), which
doesn't move, F is not null bout l is null, so one has
a zero work. No work is done unless the object moves.
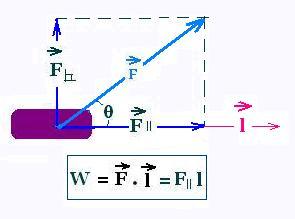
The work done by a force whose direction is perpendicular to
the displacement is null.
The work is positive when θ is
smaller than π/2.
The work is negative when θ is greater that
π/2, as when we lower a free-fall of an object by exerting an
upward force while the displacement if downward opposite to the exerted
force F.
2. Work done by a variable force
2.1. Definition
Many forces that we encounter are not constant. such as the
the force exerted on a spring that depends on the amount of
compression or stretch we do on it. For a variable force acting on
a moving object on along a straight line, say the x-axis, if the force
component Fx(x) depends only on the coordinate x, we can write:
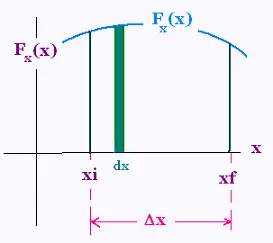
The work done on the moving object by the varying force from xi to
xf can be approximate by adding the work done along each small displacement
dx. This small displacement is take to be small enough so that the change in the force
is insignificant as x changes by dx. The elementary work dW corresponding to dx is equal to
dW = Fx(x) dx, and represents the area of the small rectangle of height
Fx(x) and base dx. Adding all this elementary works dW for the
entire displacement from xi to xf(x) dx, by integrating
from xxi to xf, we arrive at the the result:
W = ∫ Fx(x) dx
from xi to xf
Work done by a variable force
W = ∫ Fx(x) dx
from xi to xf
The work done on the moving object from xi to xf is the
area bounded by the curve and the x-axis.
If Fx(x) is constant and equals to F, then:
W = ∫ Fx(x) dx = F ∫ dx = F(xf - xi) = FΔx
from xi to xf
2.2. Examples
2.2.1. Spring force acting on a block
2.2.1.1. Hooke's law
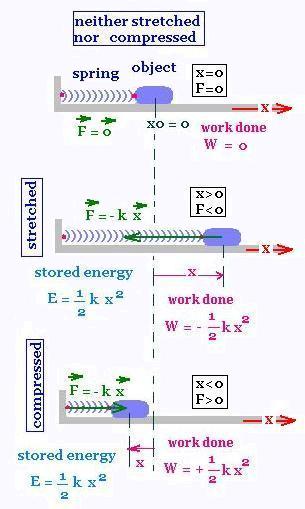
A spring fastened at one end to a fixed support and attached at the
other end at a block that can slide on a horizontal surface.At first, the spring is
in its relaxed state, that is not stretched nor compressed at the position x = 0.
The position of the block is x from this equilibrium position. The distance x represents
the amount of stretch or compression of the spring. The magnitude of the force F is proportional
to the distance x, described by Hooke's law:
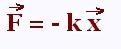
F(x) is the force exerted by
the spring on the block, and k is the spring constant of the spring. Its unit is the Newton/meter
(N/m).
If x = 0, then F = 0 and we have the equilibrium position for the block. If the spring
is extended, x is positive, so F(x) is negative, and the spring force tends to return
or restore the block to equilibrium position. Similarly, if the spring is compressed, then
x is negative, so F(x) is positive and again the spring force tends to return the block to
x = 0.
Hooke's law: spring exerts a restoring force on the block:
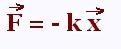
valid for displacements from equilibrium that
are small compared with the length of the spring
According to the direction of x-axis, if x is positive then F(x) is negative, and
if x is negative, F(x) is positive. Stretched or compressed, the force
always restores the block to the equilibrium position. That is the effect of restoring
force opposes the cause of compressing or stretching. The spring exerts a force on the block
that is opposite in direction to the related displacement of the block, the force is a
restoring force.
2.2.1.2. Work done by a spring on the block
The work done by a spring on the block moving from xi to xf is:
W = ∫ Fx(x) dx = ∫ (- k x) dx = -(1/2) kx2
from xi to xf
= - (1/2) k (xf2 - xi2)
Work done by force F on a spring of constant k:
W = - (1/2) k (xf2 - xi2)
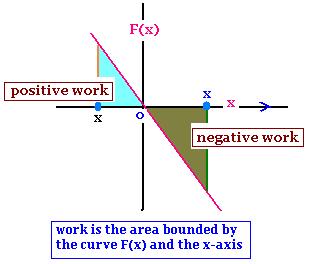
The work done by the spring on the block is negative when the spring is
stretched. It is positive when the the spring is compressed.
Example:
For a spring of a spring constant k = 3.0 kN/m , what is the work done by this spring on
an attached block if
(a) the spring is compressed by x = - 20 cm, (b) the spring compressed
from - 20 cm to - 40 cm and (c) is stretched from
x = 10 cm to 25 cm?
We have:
(a) W = -(1/2) (3000)( 0.2 x 0.2 - 0) = - 60 J
(b) W = -(1/2) (3000)(0.4 x 0.4 - 0.2 x 0.2 ) = - 180 J
Even though the displacement is the same the work done is different,
because F(x) depends always on x.
(c) W = -(1/2) (3000)( - 0.25 x 0.25 - 0.1 x 0.1 ) = - 78.75 J
2.2.2. Freely falling object
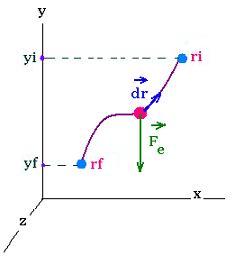
An object moves along an arbitrary path, from a point ri to a
point rf, under the gravitational force action, the work
done by this force Fe called weight on this object undergoing
an infinitesimal displacement dr is:
dW = Fe dr
Note that the gravitational force has only a y component Fe. The
y-axis is chosen vertically upward, Fe= - m g. The two other
components of Fe along x-axis and z-axis are null. Then
dW = Fe dr = - m g dy
Since the force is constant, integrating from yi to yf
gives:
W = ∫dw = ∫ ( - mg dy)= - mg ∫ dy = - mg (yf - yi)
from yi to yf
Work done by the gravitational force on a freely falling object of mass m
W = - mg (yf - yi)
The gravitational force acts down, it does a negative work on the object
when the object moves up (yf > ri) , and positive work
when the object moves down (yf < ri)
as it is restored by the gravitational force.
Notice that <the work done by the gravitational force is
independent of the path connecting the initial and final points.
3. General expression for work
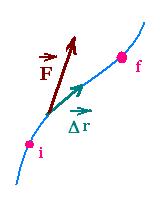
In addition to a force that varies as the object moves along a straight line,
we consider a path which is curved rather than straight. To evaluate the work
done by a force that varies in magnitude and direction, we divide the
path into several infinitesimal displacement segment Δr. This segment
is considered so small that the force vector can be considered constant and Delta;r
straight during this minute displacement. Then for each segment Δr, the
work element is : ΔW = F . Δr. For each of the segments Δr that
form the path from the initial point i to the final point f, we add the contributions
ΔW. The sum gives an approximation for the work done by the force F
for the entire path:
W = Σ F Δr
The limit of this sum is set with the number of segments tends to infinity
while the length of each displacement approaches zero. The limit of this sequence
of sums is defined as a line integral:
∫ F.dr
from the initial point to the final point f
General expression for the work done by a
varying force on an object as it moves
along any
path from the initial point i to the final point f
∫ F.dr
from the initial point to the final point f
4. Power
Power is the time rate of the related work. In other words,
Power is the time rate at which work is performed. The average power
P for a time interval Δt during which work ΔW is performed
is:
P = ΔW /Δt
The limit of this formula as Δ approaches zero defines the
power. The power is the instantaneous rate at which work is
performed:
P= dW/dt
The SI unit of power is the Watt (W) . 1 Watt = 1 J/s (Joule per second).
James Watt (1736 - 1819), had introduced the unit of horsepower to
characterize the rate at which steam engines performed work. The horsepower
(hp) is defined as equal to 746 W.
1 hp = 746 W
An alternative expression for power can be found in terms of force
and speed :
dr = v dt
P = dw/dt = d(F.dr)/dt = F .v
Power is the time rate at which work is performed
P = dW/dt = F . v
1 hp = 746 W
|
|