Dynamics
Contents
Applications
Exercises
© The scientific sentence. 2010
|
Dynamics: Conservation of energy
In Physics, a quantity is conserved when it does not change with time.
Its value at some initial instant is the same as its value
at some final instant, and at all times in between. If energy is
conserved for a system, the total amount of energy remains the same,
although if it changes in type of form. In the first chapter,
we develop the principle of conservation of energy in one
dimension and generalise it after.
1.Conservation energy: one dimension
1.2. Type of forces doing work on an object
1.2.1. Conservative forces
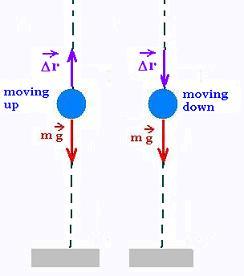
A conservative force is a force that does no net work on an object
when this object does a round-trip motion, that is the starting point is
the same as the ending point. The example is the one of the gravitational force.
An object moving up with a displacement + Δr undergoes a work
ΔWup = Fe . Δr done by the gravitational force Fe.
This work is negative, because Fe is negative and Δr is positive.
The displacement is opposite the the force.
When returning downward to its starting point, it undergoes the work ΔWdown = + Fe . Δr
This work is positive, because Fe is negative and Δr is negative.
The displacement and the the force have the same direction.
Therefore the net work done on this object by the gravitational force is:
We = Wup + Wdown = - Fe . Δr + Fe . Δr = 0
Or by another way:
W = - mg (yf - yi) = - mg (yi - yi) = 0
The gravitational force Fe is conservative.
The gravitational force Fe is conservative
The second example is the force of a spring. We have seen that
the work done on an object by a spring is:
W = -(1/2) k (xf2 - xf2)
Then for a round-trip motion, we have
W = -(1/2) k (xi2 - xf2) = 0
The force of an elastic spring is conservative.
The force of a spring is conservative.
A force is conservative if it is function only
of the coordinate that locates the object.
1.2.2. Nonconservative forces
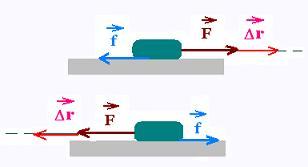
In contrast, the work done by the kinetic frictional force depends on
the direction of the object's motion, that is on the way the objects moves. This
force does not depend on where the object is as the elastic spring or gravitational force do.
On a stationary surface, if an abject slides, the direction of the frictional force
is always opposite to the velocity of the object. This force does a negative work
for both parts of the round-trip motion. The dot product Ffriction . Δr is
always negative. The net work cannot be zero. It is equal for a round-trip to:
Wnet = - 2 Ffriction.Δr.
Therefore, the frictional force in nonconservative.
A force is nonconservative if it depends
on the way the objects moves.
1.2.3. Conservative system
The forces doing work on the object are the forces due to the object
or by its surroundings. A conservative system is the system in which only conservative forces do work. Hence, the conservation energy is valid only in a conservative system. An object
moving on the floor with friction does not form a conservative system. An object
falling on the ground with non negligible air-resistance effects in not a conservative system either.
2. Conservation energy law
Consider the case of a free-fall motion of an object, in which we neglect
air-resistance effects. Then only the conservative force of gravitation does work
on the falling object: Wnet = - mg(yf - yi) We have then a conservative system. According to the work energy
theorem, the work done on the object is equal to the change in kinetic energy of the object, so:
Wnet = (1/2) mvf2 - (1/2)m vi2 , or
- mg (yf - yi) = (1/2) mvf2 - (1/2)m vi2
Rearranging related terms gives:
mg yi + (1/2)m vi2 = mg yf + (1/2) mvf2
Let's write:
mg yi = Ui , the gravitational potential energy of the object at the
position yi, and
Uf at the position yf,
(1/2)m vi2 = Ki the kinetic energy of the object at the position
yi, and
(1/2)m vf2 = Kf at the position yf
Therefore:
Ui + Ki = Uf + Kf
Ui + Ki = Uf + Kf
The work energy theorem becomes the conservation of energy.
The above equality express the conservation of the quantity
U(potential) + K(kinetic)
The gravitational potential U = mgy energy depends on the position of the moving object, and
the kinetic energy K = (1/2)m v2 depends on the speed of the moving object. Each of these
energies changes during the motion of the object, however, their sum U + K =
mgy + (1/2)m v2 will remains constant throughout the motion of the object.
The sum of the kinetic energy K and the potential energy U is defined as the
mechanical energyE .
During the motion, kinetic and potential energies are transformed into each other,
such that the mechanical energy remains unchanged.
We can then write the conservation of energy as:
Ei = Ef
Ei = Ef
Free-fall: the mechanical energy is conserved
E = mgy + (1/2)mv2
is constant
Ei = Ef
3. Net work done and potential energy
Let's recap:
Force conservative:
Wnet (round-trip) = 0
Work done by a force:
W = ∫ F . dr
from ri to rf
Work-energy theorem:
Wnet = (1/2) mvf2 - (1/2)m vi2
= Kf - Ki
Examples:
1.
Elastic spring force
F = - k x
Work done
W = - (1/2) k (xf2 - xi2)
2.
Gravitational force
F = - mg
Work done
W = - mg (xf - xi )
Application:
Gravitational force and free-fall motion:
a. Work-energy theorem:
- mg (xf - xi) = (1/2) mvf2- (1/2)m vi2
b. Conservation of energy:
The latter equation leads to:
(1/2)m vi2 + mg xi = (1/2) mvf2 + mg xf, that is:
Ki + Ui = Kf + Uf
or
Ui - Uf = Kf - Ki = Wnet
Therefore:
Wnet = Kf - Ki = - ( Uf - Ui)
Uf - Ui = - Wnet
The change in gravitational potential energy is equal to the negative
work done by the conservative gravitational force.
The change in gravitational potential energy is equal to the negative
work done by the conservative gravitational force.
Uf - Ui = - Wnet
We define then the potential energy for any conservative force as follows:
The work done by a conservative force F(r) is:
Wnet = ∫ F(r) dr
from ri to rf
Therefore:
The potential energy is:
Uf - Ui = - Wnet= - ∫ F(r) dr
The change in potential energy, Uf - Ui, due to a conservative force is
equql to the negative of the work done by this force
Uf - Ui = - ∫ F(r) dr
from ri to rf
1. Gravitational potential energy
For a moving object under gravity, from yi to yf, the change in gravitational potential
energy is:
Uf - Ui = - Wnet = mg yf - mg yi
An increase in kinetic energy corresponds to a decrease in potential energy and
vise versa.
It is important to notice that only the differences in potential energy are relevant.
The orgin, that is the zero potential energy can be set at any point of our choice,
called the refrence point. Usually, we select the reference, or level for gravitational
potential energy at at y = 0, that is U = 0 at y = 0. Having made this choice, we have:
U(x) - U(0) = mg y - mg 0 , that is
U(y) = mgy
Gravitational potential energy for an object at a point
with vertical coordinate y
U(y) = mgy
The expression of the potential energy depends on the choice of the
origin, but changes in potential energy do not.
2. Elastic potential energy
For a spring of costant k, streched oe compressed from xi to xf, the change in
elestic potential energy is:
Uf - Ui = - Wnet = (1/2) k xf2 - (1/2) k xi2
An increase in kinetic energy corresponds to a decrease in potential energy and
vise versa.
Let's select the refrence point at x = 0, that is U = 0 at x = 0, the position of
equilibrium when the spring is relaxed, neither streched not compressed.
Having made this choice, we have:
U(x) - U(0) = (1/2) k xf2 - (1/2) k 0 2 , that is
U(x) = (1/2) k x2
Elastic potential energy for a movable object attached to
a spring stretched or compressed by an amount x
U(x) = (1/2) k x2
The expression of the potential energy depends on the choice of the
origin, but changes in potential energy do not.
|
|