Physics
NYA Mechanics
Examination

Part I

Exercise 1

• (I) In the interval [0, 4] :a = rise/run = 5/2. The equation of motion is
x(t) = (1/2) (5/2) t² - 10 = (5/4) t² - 10

x(t) = (5/4) t² - 10

• (II) In the interval [5, 6] : a = rise/run = - 10/1. The equation of motion is
x(t) = (1/2) (-10/1) t² + vo t + xo.

Its derivative is:
v(t) = x'(t) = - 10 t + vo

We have v( t = 4) = 10 . So vo = 50 .

The continuity at the point (4, 10) yields: 10 = - 5 x 4² + 50 x 4 + xo . So xo = - 110

The equation of motion is
x(t) = - 5 t² + 50 t - 110.

x(t) = - 5 t² + 50 t - 110

• (III) In the interval [6, 8] : a = 0 and v = - 10 . The equation of motion is
x(t) = - 10 t + xo.

The continuity at the point (6, - 10) yields:

x(6) = - 10 x 6 + xo = x(t) = - 5 x 6² + 50 x 6 - 110 . So xo = 70

The equation of motion is
x(t) = - 10 t + 70.

x(t) = - 10 t + 70

Exercise 2

A ball is thrown towards a cliff with an initial speed of 30.0 m/s directed at an angle of 60.0 o above the horizontal.

The ball lands on the edge of the cliff 4:00 s after it is thrown. (a) What is the height of the cliff?
(b) What is the maximum height reached by the ball ?
(c) What is the ball's impact velocity ?

Answers

• (a) The equation of the motion is:

y(t) = (vo sin 60) t - (1/2) g t² + 0

y(t) = 15 √3 t - 4.9 t²

h = y(4 s) = 15 √ (4) - 4.9 (4)² = 25.5 m

h = 25.5 m

• (b) v² - vo² = 2 g h_max
(vo sin 60)² - (0)² = 2 g h_max
h_max = (vo sin 60)² / 2 g = (30 x √3/2))²/2 x 9.8 = 34.44 m

h_max = 34.44 m

• (c) The ball's impact velocity vi

yo = h_max - h = 34.44 - h = 25.5 m = 8.94 m

vy² - vo² = 2 g yo
vy² - (0)² = 2 g yo
vy² = 2 g yo = 2 x 9.8 x 8.94

vy = 13.24 m/s

vi = (vy)v² + (v cos 60^o)²
vi² = (13.24)² + (30 x 0.5)² = 20 m/s

vi = 20 m/s

tan α = v cos 60^o/vy = 1.136
α = 48.6^o

α = 48.6 ^o

Exercise 3

A 40:0N force pushes two masses, m1 = 8:00kg and m2 = 4:00kg, across a horizontal surface.

The force is directed 30^o below the horizontal, as shown in thefigure. The coefficient of kinetic friction between both masses and the surface is 0.150.

(a) Draw a free body diagram for each mass.
(b) What is the acceleration of the masses ?
(c) What is the force that m2 exerts on m1 ?

Answers:

(a) See the figure.

(b) From the free body diagrams, we have:

F12 - f2 = m2 a
f2 = ν N2 = μ m2 g

and

F cos 30 - f1 - F21 = m1 a
f1 = μ N1 = μ(m1 g + F sin 30)

F12 - μ g m2 = m2 a (1)
F cos 30 - μ(m1 g + F sin 30) - F21 = m1 a (2)

F12 = m2 a + μ g m2
F21 = F cos 30 - μ(m1 g + F sin 30) - m1 a

According to the action-reaction principle : F12 = F21,
we write:

m2 a + μ g m2 = F cos 30 - μ(m1 g + F sin 30) - m1 a

Solving for a,

m2 a + m1 a = F cos 30 - μ(m1 g + F sin 30) - μ g m2
= F cos 30 - μm1 g - μF sin 30 - μ g m2
= F (cos 30 - μsin 30) - μ g (m1 + m2)
a (m1 + m2) = F (cos 30 - μsin 30) - μ g (m1 + m2)
a = F (cos 30 - μsin 30)/(m1 + m2) - μ g

a = F (cos 30 - μsin 30)/(m1 + m2) - μ g

a = 40 (√3/2 - 0.15/2)/(8 + 4) - 0.15 x 9.8
= 5 (√3 - 0.15)/3 - 0.15 x 9.8 = 2.637 - 1.47 = 1.17 m/s²

a = 1.17 m/s²

(c) Using the relationship (1), we have:

F21 = m2 a + μ g m2 = m2 (a + μ g)
= 4(1.17 + 0.15 x 9.8) = 10.56 N

a = 10.56 N

Exercise 4

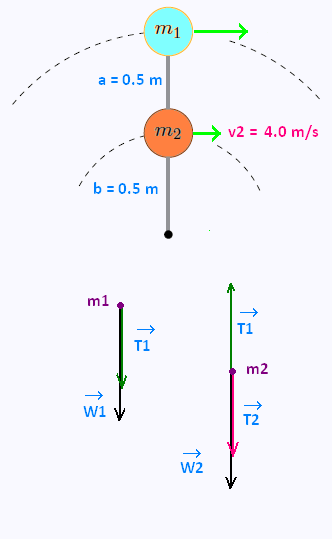
A ball of mass m1 = 4:00 kg is tied to another ball of mass m2 = 3:00 kg by a string of length 0:500 m. The two balls are swung in a vertical circle by a second string of length 0:500 m connected to m2. As the balls rotate, the strings remain parallel. At the top if the circle, m2 is moving at 4:00 m/s.

(a) Draw a free-body diagram for each mass at this instant.

(b) What is the tension in the string connecting the two balls at this instant ?

(c) What is the tension in the string connecting m2 to the centre of the circle at this instant ?

Answers:

The strings a and b remain parallel, so m1 and m2 have the same angular velocity ω.

We have:

v1 = ω x (a + b) = ω x (0.5 + 0.5) = ω
v2 = ω x b = ω x 0.5 = ω/2

v2 = 4 m/s. So v1 = 2 v2 = 2 x 4 = 8 m/s

v1 = 8 m/s

(a) See the figure.

(b) From the free body diagram of the mass m1, we have:

T1 + m1g = centripetal force = m1v1²/r. So
T1 = m1v1²/r - m1g = m1(v1²/r - g)
= 4(8²/1 - 9.8) = 216.8 N

T1 = 216.8 N

Exercise 5

The spring shown in the figure is compressed 50.0 cm and is used to launch the block, which has a mass of 100 kg. The surface is frictionless except for the final 30.0^oo incline, where the coefficient of kinetic friction is 0.150.

(a) What is the speed of the block when it reaches the valley below its starting point ?
(b) What distance does the block slide along the 30.0^oo incline before stoppin g?

Answers:

(a) Total energy (at the top of the valley) = Total Energy (at the bottom of the valley)

0 + (1/2) k x² + m gh = (1/2) mv² + 0
v² = (k/m) x² + 2gh = (8 x 10⁴/100) (0.5)² + 2 x 9.8 x 10.0 = 396

Then v = 19.89 m/s

v = 19.89 m/s

(b)The energy conservation is:

(1/2) mv² = (mg sin 30 + μ mg cos 30) x
(1/2g) v² = (sin 30 + μ cos 30) x
So
x = v²/2g(sin 30 + μ cos 30) =
396 /(2 9.8 (1/2 + 0.15 √3/2)) =
396 /(9.8(1 + 0.15 √3)) = 396/12.35 = 32.1 m

x = 32.1 m

Exercise 6

6. A 1000 kg car, travelling east at 30.0 m/s, collides with a 3000 kg truck, travelling north. After the collision, the vehicles stick together and the combined wreckage moves at 55.0 m/s north of east.

(a) What is the speed of the truck before the collision ?
(b) What percentage of the initial kinetic energy of the system is lost during the collision ?

Exercise 7

A solid wheel (made of two disks of different size) has a moment of inertia I = 0.400 kg.m2. The wheel can rotate about a frictionless axle passing through its centre. A rope wrapped around the outer radius of the wheel exerts a tangential force of magnitude 9.00 N at a distance r1 = 0.250 m from the axle. A second rope, wrapped around the inner radius of the wheel exerts a tangential force of magnitude 12.0 N at a distance r2 = 0.100 m from the axle.

(a) What is the torque due to each force and the net torque acting on the wheel ?
(b) What is the angular acceleration of the wheel ?
(c) If the wheel starts from rest, how many revolutions does it make in 12.0 seconds ?