Forces
Contents
© The scientific sentence. 2010
| Fictitious forces
They are:
Centrifugal force,
Coriolis force, and
Euler force
Fictitious means created by the imagination. Here,
in order to satisfy the Newton's second law.
1.Rotation of axes
The circular motion of a particle was described in the
circular motion section.
We have found for an orbiting mass an expression of the radial and tangential acceleration and provided the
definition of the centripetal force. The observer set on a moving mass m thought that
it exists a centrifugal force just to justify the second Newton's law. The observer
from the fixed inertial frame said that this force is just inertial or fictitious.
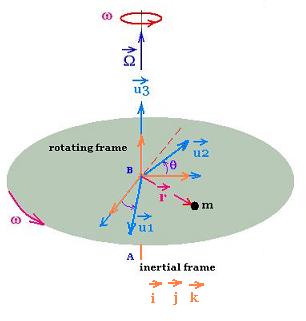
Now, we are going to set fixed in the the rotating frame B
of the mass m to see what's really going on in the obverver at the frame A point of view. Notice that the
observer in this frame B consider itself at rest. Wheras for the observer in the
inertial frame A, the frame B is rotating and it is not an
inertial frame
Now, if the mass m orbits at the angular speed ω, the frame B in which is attached
spins at the same speed ω and in the same direction. We can then set the mass
m on a rotating turntable spinning about the z-axis at the same angular velocity.
In the inertial frame A, the unit vector are i, j, and k;
the vector position of the particle of mass m is rA.
Its velocity is vA = drA/dt, and the acceleration is aA
= d2rA/dt2.
The particle of mass m rotates. Both rA, and the three unit vector
are u1, u2, and u3 rotate.
Let u1, u2 and u3 the three unit vectors of the non inertial frame B, and the mass m
has the position vector rB = x1 u1 + x2 u2 + x3 u3.
The related velocity is vB = drB/dt, and the acceleration is aB
= d2rB/dt2.
We can express any vector such as vector position, velocity, and acceleration of the
particle in the frame B in the base (u1,u2,u3) and then
transform then in the base (i,j,k) of the frame A.
After a rotation θ = ωt, about the z-axis,the unit vectors
rotate counterclockwise:
rA → x1 u1 + x2 u2 + x3 u3
u1 → u1 = cos ωt i + sin ωt j (1)
u2 → u2 = - sin ωt i + cos ωt j (2)
u3 → u3 = u3 (no change) (3)
The derivative with respect to time gives:
du1/dt = - ω sin ωt i + ω cos ωt j
du2/dt = - ω cos ωt i - ωt sin ωt j
The vector Omega; = ω k can be written Ω = 0 i + 0 j + ω k .
Hence:
Ω x u1 = ω (0,0,1) x (cos ωt, sin ωt, 0)
ω(- sin ωt i + cos ωt j + 0 k) = ω du1/dt = u2
Ω x u1 = ω du1/dt = u2 (4)
Similarly,
Ω x u2 = ω ω (0,0,1) x (- sin ωt, cos ωt, 0) =
ω ω(- cos ωt i - sin ωt j + 0 k) = - ω du2/dt = - u1
Ω x u2 = ω du2/dt = - u1 (5)
Similarly,
Ω x u3 = 0 (6)
Ω x u1 = ω du1/dt = ωu2
Ω x u2 = ω du2/dt = - ω u1
Ω x u3 = 0
2. Velocity of the particle
We will find the expression of the velocity of the
particle in the frame B, and then in the frame A.
The corresponding velocity of the point mass m is
vA = drA/dt = (dx1/dt )u1 + x1 du1/dt + (dx2/dt)u2 + x2 du2/dt + (dx3/dt)u3 + x3 du3/dt
vA = v1 u1 + x1 du1/dt + v2 u2 + x2 du2/dt + v3 u3 + x3 du3/dt
The particle of mass m moves on the plane, so x3 = v3 = du3/dt = 0.
Using the relation (4) (5) and (6), we get:
drA/dt = v1 u1 + x1 (Ω x u1) + v2 u2 + x2 ( Ω x u2 )
v1 u1 + v2 u2 = vB
x1 (Ω x u1) + x2 (Ω x u2) = ω(x1 u2 - x2 u1) = Ω x r
Therefore:
drA/dt = vA = vB + Ω x r (7)
drA/dt = vA = vB + Ω x r
3. Acceleration of the particle
The corresponding acceleration is:
aA = dvA/dt + d(Ω x r)/dt
dvA/dt = a1 u1 + v1 du1/dt + a2 u2 + v2 du2/dt + a3 u3 + v3 du3/dt =
= a1 u1 + a2 u2 + v1 du1/dt + v2 du2/dt + 0 =
= aB + v1(Ω x u1 )+ v2(- Ω x u2 ) or =
aB + v1(u2) + v2(- u1) = aB+ Ω x v
d(Ω x r)/dt = Ω x (dr/dt) + (Ω/dt) x r
Using (7), we find:
Ω x ( v + Ω x r) + (Ω/dt) x r =
Ω x v + Ω x Ω x r + (Ω/dt) x r =
Therefore:
aA = aB + Ω x v + Ω x v + Ω x Ω x r + (Ω/dt) x r =
aB + 2Ω x v + Ω x (Ω x r) + (Ω/dt) x r
aA = aB + 2Ω x v + Ω x (Ω x r) + (Ω/dt) x r
4. Related forces
Let's multiply by the mass of the particle, the two hands of the found equality, we get
the following forces:
FA = FB + Fco + Fce + Feu
Applying Newton's second law in the frame B, gives:
FB = FA + Fco + Fce + Feu
Where:
FA = - m aA is the force acting on the particle in the frame A
FB = m aB is the force acting on the particle in the frame B
Fco = - 2 mΩ x v is the force of Coriolis acting on the particle in the frame B
Fce = - m Ω x (Ω x r) is the centrifugal force acting on the particle in the frame B
Feu = - m (Ω/dt) x r is the Euler force acting on the particle in the frame B
The three forces Fco, Fce, and Feu are associated with rotation.
They are called
inertial forces, or pseudo-forces, or fictitious forces. They are real (in frame
A), but they are fictitious forces in the rotating reference frame B. These forces
are just apparent in a non-inertial reference frame and do not come from
any physical interaction between objects.
4.1. Centrifugal force
The centrifugal force Fce = - m Ω x (Ω x r) is directed
along the r direction and opposite to the centripetal force.
For an observer on the mass m, the centrifugal force is an outward force
that balance the centripetal force in order to satisfy Newton's second law.
4.2. Coroilis force
The Coriolis force Fco = - 2 mΩ x v curves
the trajectory of the rotating particle and exerts a torque on it.
In our Earth rotating reference frame, we encountere all the time the effects
of this force, but they are small, because the angular speed by which
the earth spins is small, of value ω = 7.0 x 10-5 rad/s.
For a n object of mass m = 10.0 kg moving horizontally at a speed v = 10.0 m/s, the outward Coriolis
force curves its path toward a direction perpendiculary to the plane North x West-East
by a force of 2 m Ωv = 2 . 10 . 7.0 x 10-5 . 10 = 1.4 x 10-2 kg.m/s2
= 0.014 N, that is about the gravitational force exerted on an object of mass equal
to 1 gram.
4.2. Euler force
The Euler force Feu = - m (Ω/dt) x r
appears when the rotation of the rotating reference frame is not uniforme, that is
the angular velocity ω varies in time in magnitude or in direction such as
a precession.
|
|