Gravitational potential energy

1. Gravitational force

When an object is close to earth's surface, the gravitational potential energy of an object of mass m at the height y from the surface is:

U(y) = m g y


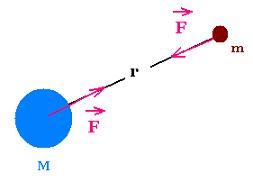
For an object such as a satellite, far from the earth, another expression for the gravitational potential energy is needed.

Newton's law of universal gravitation relates the attractive force of interaction of two objects of mass M and m distant at r from each other center. The magnitude of this force is:

F = G M m /r²

2. Work done by the gravitational force

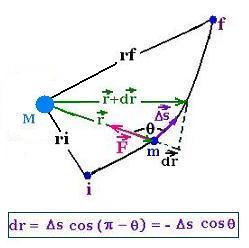
Taking any path from i to f, the gravitational force exerted on the object of mass m does an elementary work ΔW when the position vector changes with Δr. The object of mass m moves with respect to the second object of mass M. The force is directed along the line joining the two objects.

For a small displacement Δs corresponding to Δr = Δs cos θ, we have:
ΔW = F . Δs = |F| |Δs| cos θ = - F Δr
Notice that the gravitational force is conservative, the work done by this force does not depend on path. This feature is set by the fact that the perpendicular component of the force does not do work.

The total work done from i to f is:

W = ∫ dW = ∫ - F dr = ∫ - (G M m /r²) dr =
from ri ti rf

= - G M m ∫ dr/r² = - G M m [-1/r] = G M m /r
from ri ti rf
W = G M m (1/rf - 1/ri)

W = G M m (1/rf - 1/ri)

3. Gravitational potential energy

The change in gravitational potential energy Uf - Ui is the negative of the work done by the gravitational force on the object, that is:
Uf - Ui = - G M m (1/rf - 1/ri)


The convenient choice to determine the expression of the potential energy is to set it zero when the separation is infinity, so U(∞) = 0. Therefore:

U_g (r) = - G M m/r

4. Example: Satellite on a circular orbit

If the object of mass m is a satellite orbiting the earth of mass m_e, at the speed v, and the only force that act on the satellite is the gravitational force, writing the conservation of mechanical energy gives;

E + K + U = (1/2)m v² + (- G m_em/r)

As r increases, the potential energy increases, then the kinetic energy decreases. Closer to the earth, the satellite moves rapidly.

For the special case of a circular orbit, the potential energy remains constant, so the kinetic energy is. The centripetal force is provided by the gravitational force.
Newton's second law for the satellite, ΣF = m a gives:
mv² /r = G m_e m /r²
Therefore:
v² = G m_e/r

The kinetic energy is:
K = (1/2) mv² = (1/2) G m_e m /r = - (1/2) U

In magnitude the kinetic energy is one-half the potential energy
E = K + U = - (1/2) U + U = (1/2) U
E = - (1/2) G m_em /r

5. Escape speed

The mechanical energy of the satellite is negative. It due to the fact that U is negative and the fact that U = 0 at the infinite separation of the two objects. We can never be beyond infinity to have this energy positive, so this energy is never positive. At least it is equal to zero once the satellite approaches infinity.

The kinetic energy is always positive.

As r approaches infinity, U approaches zero, that is the minimum value that can take the potential energy U, the kinetic energy approaches zero as well but still positive, so K is positive and E = U + K is positive. In other expressions, a free object (U = 0) has more energy than the satellite has, we say that the satellite is bounded to the earth.
The minimum required energy to free the satellite of earth's influence is called the binding energy. For the satellite on a circular orbit about the earth, at the position r, it is |E| = E_b = (1/2) G m_em /r.

Suppose we give an object of mass _o at the distance ri from the earth's surface, a speed vi. Its kinetic energy is K = (1/2) m_ovi² and potential energy U = - G m_e m_o/ri , so its mechanical energy is:

E = K + U = (1/2) m_ovi² - G m_e m_o/ri

At the infinity, the object will be free with at least 0+ kinetic energy, so let's write at the infinity, E = 0. Therefore:
(1/2) m_ovi² - G m_e m_o/ri
and
(1/2) vi² = G m_e /ri
or
vi = [2 G m_e/ri]^1/2
That is the escape speed. It doesn't depend on the mass of the escaping object.