Physics: Kinematics
displacement
velocity
acceleration
graphs

1. Constant acceleration

When an object has an initial velocity vi and that is moving in a straight line with constant acceleration a, the following equations connect the final velocity vf and displacement x in a given time t.

• vf = vi + a t
• x = (vi + vf)t/2
• x = vi t + (1/2) a t²
• x = vf t - (1/2) a t²
• vf² = vi² + 2 a x


Note: These equations cannot be used if the acceleration is not constant.

2. Variable acceleration

In the case that the acceleration is not constant, to determine a variable such as timre (t), displacement (x), velocity (v) or acceleration (a) from the anothers we use:

• The integral calculus, or
• The area under the curve of velocity or acceleration with respect to time through a given graph.

Graphs can often be used to find displacement from velocity-time graph, and velocity from acceleration-time graph.

This is due to:

• The gradient of a displacement-time graph is velocity: v = dx/dt, and
• The gradient of a velocity-time graph is acceleration: a = dv/dt.


By using geometrical figures area formulas':

The area under a velocity-time graph
indicates the displacement .

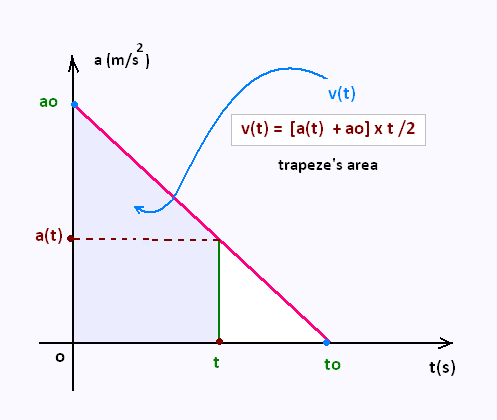
The area under an acceleration-time graph
indicates the velocity .

3. Velocity from acceleration

4. Displacement from velocity