Kinematics: projectile in two dimensions motion

1. Definitions:

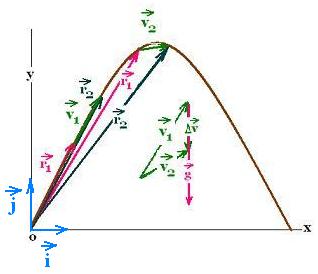
A projectile is defined as an object thrown from a certain surface (Earth) moving against a gravity. A golf ball is a projectile. The effect (how it behaves) of the motion of a projectile is caused, set and dictated by the presence of gravity. The gravitational acceleration "g" (deceleration) is a vertical acceleration, and directed downward. The projectile motion is not decelerated because there is a change in the velocity, it is accelerated because it is present in the gravity. That implies the change in the velocity Δ⃗v. ( "g" exists → Δ⃗v exists). Since ⃗g is directed vertically downward, so does Δ⃗v. Thus there is no horizontal component for the acceleration. If ⃗a is the acceleration of the object, ⃗a = ⃗a_x + ⃗a_y = 0 + ⃗a_y = ⃗a_y = a_y ⃗j = - ⃗g = - g ⃗j = - 9.81 ⃗j.

2. Projectile motion: ballistic trajectory

If ⃗a_x = 0, that is d⃗v_x/dt = 0, then: ⃗v_x = constant = ⃗v_xo. Hence: ⃗x = ⃗v_xo t + ⃗x_o.
At t = 0, we have ⃗x = o, thus ⃗x_o = 0, Hence:

The component of the projectile motion, along the "x" axis is:

⃗x = ⃗v_xo t = v_xot ⃗i

Similarly, If ⃗a_y = - ⃗g = constant, that is d⃗v_y/dt = constant, then: ⃗v_y = - ⃗g t + constant = - ⃗g t + ⃗v_yo. Hence: ⃗y = - (1/2) ⃗g t² + (⃗v_yo) t + constant2 = = - (1/2) ⃗g t² + (⃗v_yo) t + ⃗y_o.
At t = 0, we have ⃗y = o, thus ⃗y_o = 0, Hence:

The component of the projectile motion, along the "y" axis is:

⃗y = - (1/2) ⃗gt² + (⃗v_yo) t = - (1/2) g t² ⃗j + (v_yo t) ⃗j

Eliminating the parameter time "t" in the two above equations can be as follows: From the first equation, we have t = x/ v_xo. Substituted in the second equation, gives:
y = - (1/2) g (x/ v_xo)² + v_yo (x/ v_xo) = - [(1/2) g / v_xo²] x² + [v_yo/ v_xo] x.

y = - [(1/2) g / v_xo²] x² + [v_yo/ v_xo] x
Which is an equation of a parabola.

The range of the path (parabola) corresponds to: - [(1/2) g / v_xo²] x² + [v_yo/ v_xo] x = 0; that gives: x_r = 2[v_yo v_xo]/g

The range is: x_r = 2v_yo v_xo/g

The maximum corresponds to:
dy/dx = 0, that is - [ g / v_xo²] x + [v_yo/ v_xo] = 0. Hence:
x = v_yo v_xo / g , and y = y = - [(1/2) g / v_xo²] (v_yo v_xo / g)² + [v_yo/ v_xo] (v_yo v_xo / g) =
- (1/2) (v_yo ²/g) + v_yo²/g = (1/2) v_yo ² / g

Coordinates of the maximum point (height of the trajectory):
x_m = v_yo v_xo/g         y_m = v_yo ²/2g

3. Projectile motion: polar coordinates

In polar coordinates, we have:

⃗x = ⃗v_xot = (v_o cosθ t) ⃗i
⃗y = - (1/2) g t² ⃗j + (v_o sinθ t) ⃗j
y = - [(1/2) g / v_o² cos²θ] x² + [v_o tgθ] x
x_m = v_o² cosθ sinθ / g = (v_o²/2g) sin 2θ
y_m = (v_o ²/2g) sin² θ


At θ = 45^o:

⃗x = (2^1/2/2)v_o t ⃗i
⃗y = - (g/2) t² ⃗j + (2^1/2/2)v_o t ⃗j

y = - [(g/4) / v_o²] x² + (1/2)v_o x
x_m = v_o²/2g
y_m = v_o ²/4g

4. Projectile Motion: Particular cases:

4.1. One dimension motion: elevation θ = 0

For a horizontal launch: ⃗x = ⃗v_xot = v_ot ⃗i. The velocity ⃗v = d⃗x/dt = v_o⃗i is constant; and the acceleration d⃗v/dt is null.

4.2. One dimension motion: elevation θ = π/2

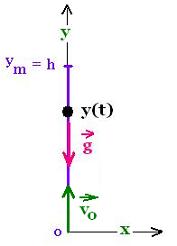For a vertical launch:
⃗x = 0
⃗y = [- (1/2) g t² + v_ot] ⃗j
x_m = 0
y_m = v_o ²/2g


y = - (1/2) g t² + v_ot
y_m = v_o ²/2g


The time of flight t_f for this vertical launch can be found as follows:
y = y_m = h = - (1/2) g t² + v_ot
This quadratic equation can be written:
(1/2) g t² - v_ot + h = 0
Which has the following two roots:
t_f1 = [v_o + (v_o² - 2gh)^1/2]/2
t_f2 = [v_o - (v_o² - 2gh)^1/2]/2

Limit case:
(v_o² - 2gh)^1/2 = 0. That is v_o = (2gh)^1/2
Then: t = v_o/g, that corresponds to the height of the trajectory.

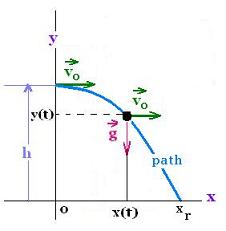
4.3. Two dimensions motion: Free-fall with initial velocity:

At the height "h", if an an object is launched with a velocity ⃗v_o directed at an angle θ with respect to the horizontal line, this object undergoes a free-fall effect.
If we decompose the vector velocity ⃗v_o into two perpendicular components ⃗v_oxt = ⃗v_o cos θ and ⃗v_oy = ⃗v_o sin θ, we can write:
- Along the "x" axis:
x(0) = 0, the initial velocity is ⃗v_0x = v_0x ⃗i = v₀cos θ ⃗i, and there is no acceleration ⃗a_x = 0. Hence:
⃗x(t) = ⃗v_oxt
x(t) = v_oxt = v_o cos θ t
- Along the "y" axis:
y(0) = h, the initial velocity is ⃗v_0y = v_0y ⃗j = v₀sin θ ⃗j, and the acceleration is imposed by gravity: ⃗a_y = - g⃗j. Hence:
⃗y(t) = [h + v_oy t - (1/2) g t²]⃗j
y(t) = h + v_oy t - (1/2) g t² = h + v_o sinθ t - (1/2) g t²
y(t) = h + v_o sinθ t - (1/2) g t²

The period of time lasted by the motion can be found as follows:
y(0) = 0, that is:
h + v_o sinθ t_l - (1/2) g t_l²] = 0
(1/2) g t_l² - v_o sinθ t_l - h = 0
This quadratic equation has the following root:
t_l = ( v_o + [v_o² sin²θ + 2gh]^1/2)/g;

The range is then equal to: x_r = t_l v_o cosθ

4.4. Two dimensions motion: Range and maximum height:

1. Along the x-axis:

acceleration a = 0
x_o = 0
x = v_ox t = v_o cosθ t
x = v_ox t = v_o cosθ t

2. Along the y-axis:

acceleration a = - g = - 9.80 m/s²
y_o = h_o
y = y_o + v_oy - (1/2)g t² = h_o + v_osin θ - (1/2)g t²

y = h_o + v_osin θ t - (1/2)g t²

y = h_o + v_osin θ t - (1/2)g t²

3. At h_max:

we have v_x = v_ox, and v_y = 0, so
0² = v_oy² + 2 (- g) (h_max - h_o), that is:
0 = v_oy² - 2 g (h_max - h_o). Therefore:
h_max = [(v_osin θ)²/2g] + h_o

h_max = [(v_osin θ)²/2g] + h_o

h_max = [v_osin θ)²/2g] + h_o

4. At x = r:

y = 0 , then:
y = h_o + v_osin θt - (1/2)g t₂ = 0

4.1. Simple method:

Solve for the time t. We find t₊ and t_- .
The convenient solution is t = t₊.
Using t₊, we find:

x = r = v_ox t₊ = v_ocosθ t₊
The range is r = v_ocosθ t₊

r = v_ocosθ t₊

4.2. Other method:

substitute x = v_oxt = v_o cos θ t in the equation:
y = y_o + v_o sinθ t - (1/2) g t² , and find:
y = y_o + tanθ x - (1/2) g (1/v_ocos θ)² x²

When y = 0, we solve for x the quadratic following equation:
0 = y_o + tanθ x - (1/2) g (1/v_ocos θ)² x², and find the range x = r.

In the case of y_o = 0 , we have:
0 = tanθ x - (1/2) g (1/v_ocos θ)² x²
Hence:
x = 0, or
tan θ - (1/2) g (1/v_ocos θ)² x
That is:
x = r = 2 tan θ (v_ocos θ)²/g

x = r = 2 tan θ (v_ocos θ)²/g

5. Particular cases:

5.1. The initial velocity is null:

v_o = 0 we have a free-fall motion.
The equation of the motion is:
y(t) = h - (1/2) g t² = h + v_o sinθ t - (1/2) g t².
The period of time lasted by the motion is determined as follows:
y(t) = h - (1/2) g t² = 0.Then:
t_l = (2h/g)^1/2

The range is then equal to: x_r = 0

5.2. The initial velocity is horizontal:

v_oy = 0 , then v_ox = v_o. We have also a free-fall motion.
The equation of the motion is:
y(t) = h - (1/2) g t²
Equating to zero: y(t) = h - (1/2) g t² = 0 gives the period of time lasted by the motion:
t_l = (2h/g)^1/2

The range is then equal to: x_r = t_lv_o = (2h/g)^1/2v_o

5.3. The initial velocity is vertical:

v_ox = 0 , then v_oy = v_o. We have also a free-fall motion.
The equation of the motion is:
y(t) = h + v_ot - (1/2) g t²
Equating to zero: y(t) = h + v_o - (1/2) g t², that is (1/2) g t² - v_o - h = 0 gives the period of time lasted by the motion:
t_l = ( v_o + [v_o² + 2gh]^1/2)/g
The range is then equal to: x_r = t_lv_o

Remark:
The period of time lasted by the motion is the same whatever the initial velocity is null or horizontal.

5.4. One dimension motion: Mixed: Free-fall and vertical initial velocity:

The object A moves upward with a velocity V_Ao. The Kinematic equations give for its position :
y_A (t) = 0 + V_Ao t - (1/2) g t². For the object B, we have : y_B (t) = h + 0 - (1/2) g t².
At a certain time t_m, the two objects will have the same position from the ground (axis x). We can then write:
y_A (t_m) = y_B (t_m); that gives:
V_Ao t_m - (1/2) g t_m² = h + 0 - (1/2) g t_m², that yield:
V_Ao t_m = h , then:

t_m = h /V_Ao

The same position has the value:
y_A = y_B = h - (1/2) g [h /V_Ao]²

It could happen that the object A turns back before meeting the object B. A turns back at the time given by zeroing the derivative of the expression of its position: y_A (t) = V_Ao t - (1/2) g t²; that is:
d[y_A (t)]/dt = V_Ao - g t_b = 0 , that yields:
t_b = V_Ao / g In fact, they will meet at least if t_b is equal or greater than t_m that is : t_b >= t_m, then:
V_Ao / g >= h /V_Ao, or V_Ao² >= gh . That is:
V_Ao >= [gh ]^1/2

Example:
If h = 80 m, we have: V_Ao >= [9.81 x 80 ]^1/2 = 28 m/s.
An initial speed less than this value is not sufficient for the object A to meet the object B. The latter will turn back without meeting the former and fall on the ground before it does.